LING525/CIS558
Some other approaches to modeling time-series data
Introduction
We often have a sampled function of time (or space) that was generated by an underlying process with relatively few parameters -- or at least relatively few that are of interest to us. Here's an example of an F0 contour for a sequence of Chinese syllables whose lexical tones are rising+falling+low+falling, for example:
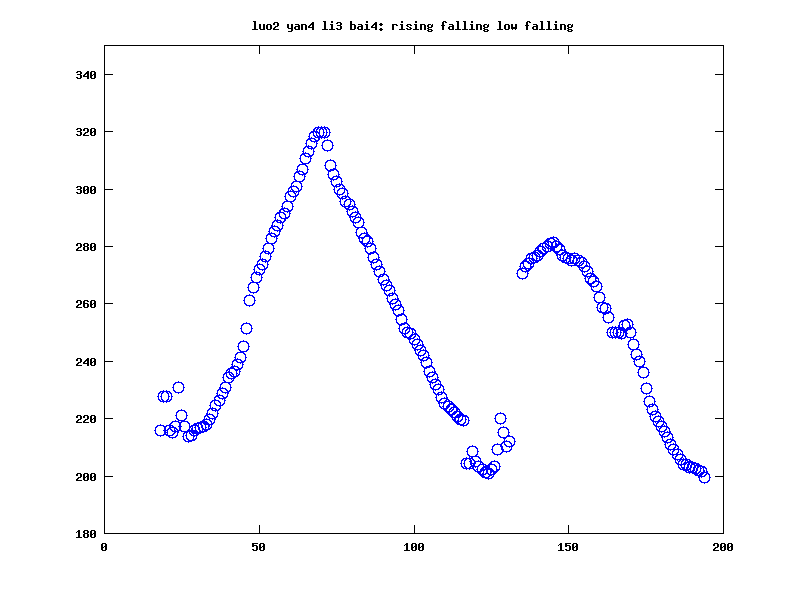
Such sequences of values are relatively smooth, so it's clear that the number of degrees of freedom is less than the number of samples we're using to see the pattern. But how should we determine what's really going on? Or at least, how should we use the available numbers to classify or analyze such sequences, to characterize properties associated with their causes or effects, and so on?
One obvious way to proceed is to schematize the sampled-time function in a way that makes sense to us, so as to reduce the apparent degrees of freedom to something more manageable. As a simple example, in this case we might use a piece-wise linear approximation, with linear interpolation between F0 targets at specified time points. If we allocate two targets per tone, that would reduce 194 sampled F0 values to 8 time/value pairs; if we used some automatic method of bottom-up contour linearization, without knowing the tonal transcriptions, we'd end up with a similar number of numbers.
There are a dozen or so methods of schematization that have been used for representing pitch contours. Most of them are quite a bit more complicated than this. A few examples (with rather different goals, assumptions, and degrees of generality) are Prosogram, the (Fujisaki) Command/Response model, MOMEL/INTSINT(code here), Stem-ML (see also here), the Superposition/Alignment model, Tilt, etc.
Several papers from the Oxford University Phonetics Lab used orthogonal polynomials to create a low-dimensional representation of fairly smooth, fairly simple sampled functions. This representation is then used to provide independent variables for use in simple models to predict intonational contour type, perceived prominence, etc.. [e.g. Esther Grabe et al., "Quantititative modeling of intonational variation", Proceedings of SASRTLM (Speech Analysis and Recognition in Technology, Linguistics and Medicine) 2003; Greg Kochanski et al., "Loudness predicts prominence: fundamental frequency lends little", JASA 2005); code here]
The goal of these lecture notes is to explore various ways of accomplishing the same sort of thing. We'll start with orthogonal polynomials, and then go on to try things like Functional PCA. But rather than use real-world data, we'll start with some synthetic data where we know what answer we're looking for.
A first synthetic problem
We have a singular triangular obtrusion that can vary in offset, width, and height:

We can sample this function at any desired granularity (as long as there are enough samples to capture the pattern). It's plausible to add some noise (and here we switch to 100-element vectors rather than 1000):

(The function used to create these patterns is here. Note that the underlying fake-data vector has been smoothed before adding the noise, via convolution with a short bell-shaped function, mainly for aesthetic reasons...)
Now let's try representing such sequences as a linear combination of orthogonal polynomials. Among the various available alternatives, we might pick "Chebyshev polynomials". A bit of poking around on the web finds us ChebyshevPoly.m, which we can use to write a simple function to create the desired number of basis vectors for the desired number of vector elements:
NPOLY = 9;
COP2 = corthpoly2(NPOLY,NN);
plot(COP2');
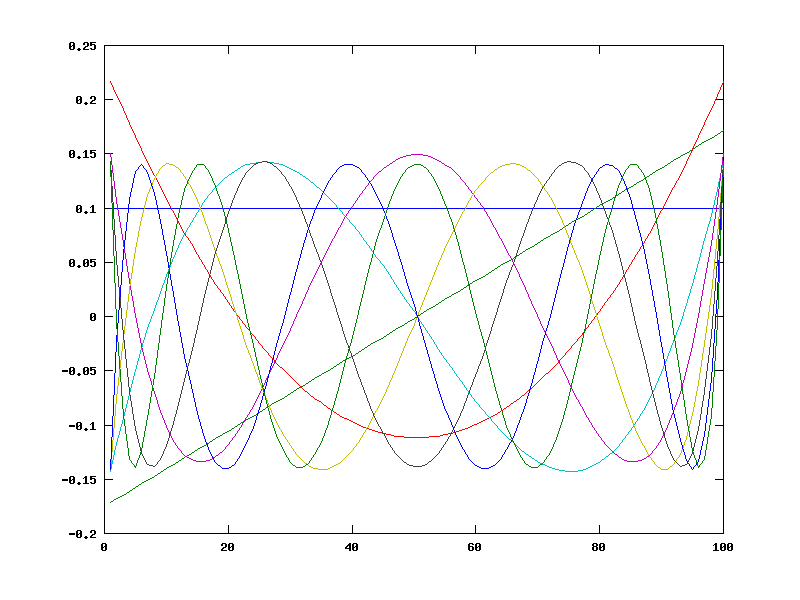
We can use matlab/octave "matrix left divide" to find the coefficients that do the best least-squares job of representing an instance of our fake-data function:
orig = makefake(.5*NN, .4*NN, 90, NN, 0);
orig1 = orig + randn(NN,1)*10;
% orig1 = COP2'*x; so COP2'\orig1 = x
x = COP2'\orig1;
synth1 = COP2'*x;
plot(1:NN,orig1,'b', 1:NN,orig,'k', 1:NN,synth1,'r')
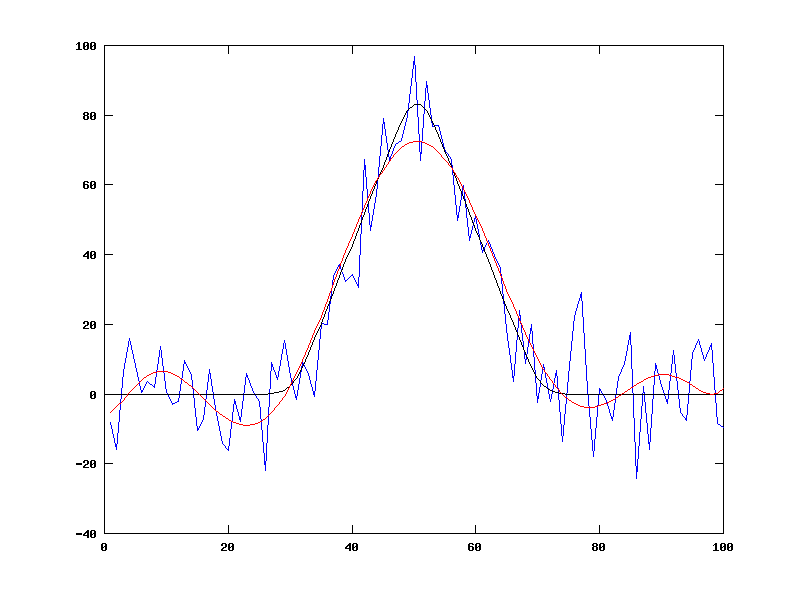
As you can see, this does a decent job of representing the various instances of our family of fake-data functions, using only 9 parameters rather than 100 (or 1,000 or whatever):
orig1 = makefake(.3*NN, .4*NN, 90, NN, 10); orig2 = makefake(.7*NN, .4*NN, 90, NN, 10); orig3 = makefake(.5*NN, .7*NN, 90, NN, 10); orig4 = makefake(.5*NN, .4*NN, 110, NN, 10); orig5 = makefake(.5*NN, .4*NN, 50, NN, 10); orig6 = makefake(.5*NN, .4*NN, -100, NN, 10);synth1 = COP2'*(COP2'\orig1); synth2 = COP2'*(COP2'\orig2); synth3 = COP2'*(COP2'\orig3); synth4 = COP2'*(COP2'\orig4); synth5 = COP2'*(COP2'\orig5); synth6 = COP2'*(COP2'\orig6);subplot(2,3,1); plot(1:NN,orig1,'b',1:NN,synth1,'r'); ylim([-130 130]) subplot(2,3,2); plot(1:NN,orig2,'b',1:NN,synth2,'r'); ylim([-130 130]) subplot(2,3,3); plot(1:NN,orig3,'b',1:NN,synth3,'r'); ylim([-130 130]) subplot(2,3,4); plot(1:NN,orig4,'b',1:NN,synth4,'r'); ylim([-130 130]) subplot(2,3,5); plot(1:NN,orig5,'b',1:NN,synth5,'r'); ylim([-130 130]) subplot(2,3,6); plot(1:NN,orig6,'b',1:NN,synth6,'r'); ylim([-130 130])

It's still 3 times as many degrees of freedom as the underlying generating function used, but it's better.
If you feel like exploring further, you could try a simple experiment like this:
Assume that the underlying parameters of offset, width and height are used to encode 8 discrete categories, representing the binary features early/late, positive/negative, wide/narrow. Thus 111 would be late+negative+narrow, 010 would be early+negative+wide, etc.
Take the mean values to be (say) early = 0.3, late = 0.7; positive = 100, negative = -100; wide = 0.4, narrow = 0.2. Create a (sufficiently large) sample of fake data, using something like makefake.m, and adding a suitable amount of noise. (Note that you may need to insert checks to avoid indices below 1 or above NN.)
Create a simple Gaussian classifier, using your sample of training data to estimate mean vectors and covariance matrices for each of the eight classes, and testing on an (independently created) test sample by calculating the mahalanobis distance to each to the class centroids, and choosing the closest one.
Do this using the original sampled data. Note that to the full covariance matrix requires you to estimate 100^2 (or 1000^2) numbers. In the real world, you probably wouldn't have enough data to do this; so use a diagonal covariance matrix instead (i.e. just the variances; all off-diagonal elements are zero).
Do the same things with the coefficients from the COP fit. Here you need only 9^2 (or 6^2 or 20^2) parameters for the full covariance matrix, so try it.
How well do the two methods work? Why?
Here's a slightly more compicated experiment. It's been claimed that in Sweden, there's geographical variation in the alignment of pitch-accent patterns with syllable sequences, superimposed on a difference between two lexically-distinct pitch-accent types (called Accent I and Accent II) that is also realized mainly by alignment:
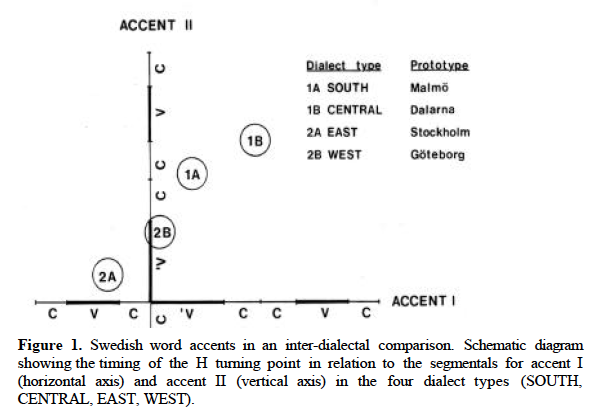
Similar geographical gradients have been reported for other languages. So we're going to look at pseudo-Swedish, in which a one-dimensional geographical gradient (from pseudo-north to pseudo-south) maps onto a gradient delay in our triangular obtrusion. This is superimposed on a binary opposition between positive obtrusions and negative ones (which however do not differ in time-offset). Obtrusion width varies randomly.
% "south" = 0 to "north" = 1
NTRIALS = 100; NN = 100;
Geo = (0:(1.0/(NTRIALS-1)):1)';
% Peak location variable is 0.3 + 0.4*Geo + noise
GEONOISE = 0.03;
Offset = NN*(0.3 + 0.4*Geo + GEONOISE*randn(NTRIALS,1));
% Heights -- half 100, half -100, alternating even and odd trials, + noise
HVAL=100; HNOISE = 10;
Height = HVAL*repmat([1;-1],[NTRIALS/2 1]) + HNOISE*randn(NTRIALS,1);
% Width -- 40 + noise
WVAL = 40; WNOISE=5;
Width = repmat(WVAL,[NTRIALS 1]) + WNOISE*randn(NTRIALS,1);
% Create NTRIALS sampled time functions:
DNOISE = 10; Data = zeros(NTRIALS, NN);
for n=1:NTRIALS
Data(n,:) = makefake(round(Offset(n)), round(Width(n)), Height(n), NN, DNOISE);
endfor
%
figure(1)
plot(Data(1:9:100,:)')

Now we fit the COP parameters to these time-functions:
NPOLY = 9;
COP = corthpoly2(NPOLY,NN);
% orig1 = COP2'*x
Para = zeros(NTRIALS, NPOLY);
for n=1:NTRIALS
Para(n,:) = COP'\Data(n,:)';
endfor
To verify that it worked, let's plot the first 50 (pseudo-south) re-synthesized time-functions and the last 50 (pseudo-north):
subplot(1,2,1)
plot((Para(1:50,:)*COP)')
subplot(1,2,2)
plot((Para(51:100,:)*COP)')

How do the COP coefficients reflect the underlying structure of the data? Here are some scatterplots of coefficient 1 against coefficient 2, for various subclasses of data, which will give you a hint:
rrx = [min(Para(:,1)) max(Para(:,1))]; rry = [min(Para(:,2)) max(Para(:,2))];
subplot(2,2,1)
scatter(Para(1:2:40,1), Para(1:2:40,2)); xlim(rrx); ylim(rry);
title('Odd (positive) tokens 1-40 (Southern)'); xlab('Coef 1'); ylab('Coef 2')
subplot(2,2,2)
scatter(Para(2:2:40,1), Para(2:2:40,2)); xlim(rrx); ylim(rry);
title('Even (negative) tokens 1-40 (Southern)'); xlab('Coef 1'); ylab('Coef 2')
subplot(2,2,3)
scatter(Para(61:2:100,1), Para(61:2:100,2)); xlim(rrx); ylim(rry);
title('Odd (positive) tokens 61-100 (Northern)'); xlab('Coef 1'); ylab('Coef 2')
subplot(2,2,4)
scatter(Para(62:2:100,1), Para(62:2:100,2)); xlim(rrx); ylim(rry);
title('Even (negative) tokens 60-100 (Northern)'); xlab('Coef 1'); ylab('Coef 2')

We could use a simple technique to predict the north-to-south gradient values from the COP coefficients fit to the sampled time functions. Suppose that we determined the regression parameters from a suitable set of fake "training data" (where the geographical location is known), and tested their efficacy on some (different) fake "test data" (where we compared our predictions of geographical location against the "truth". It should be clear that this will work well.
What if we tried to do the same thing using the sampled-data values themselves? In other words, rather than 9 unknowns (or 10 including an intercept term), we have 100 (or 101). How well do you think this would work?
How could we modify the generating procedure to make prediction from the sampled data values harder or easier? Similarly, what changes in the generating procedure would make prediction from the COP coefficients harder or easier?
Simple "functional principal components analysis"(FPCA)
We will use data gathered by Jiahong Yuan for his thesis, in order to explore some of the ideas in John A. D. Aston et al., "Linguistic pitch analysis using functional principal component mixed effect models", J. Royal Stat. Soc.: C, 59 (2): 297–317, 2010.
Our dataset starts with 999 8-syllable utterances from 8 speakers. Since Prof. Yuan's goal was to model F0 contours (using an interesting technique different from the one being explored here), the utterances were composed of all voiced sounds, including a minimum number of voiced stops and as many nasals, liquids and glides as possible. A typical utterance:
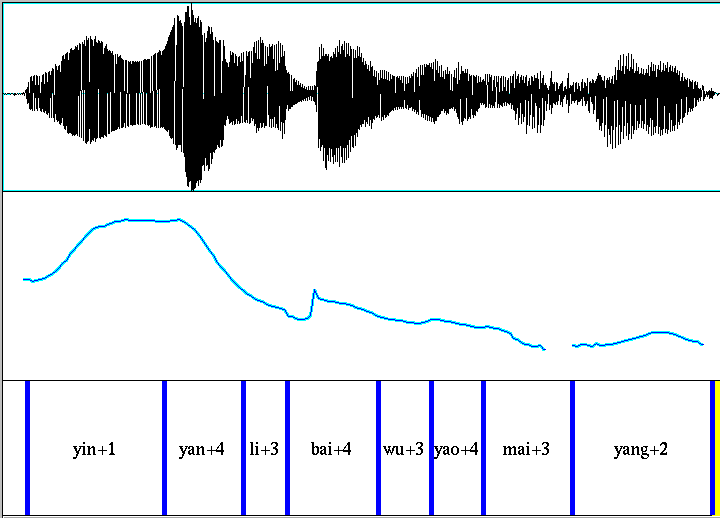
Each recording was supplied with a syllable-level segmentation, as shown in the Praat screenshot above.
I pitch-tracked all of the original .wav files (using the ESPS get_f0 function), pulled out the time-samples corresponding to each syllable, and re-sampled these sequences so that each one had exactly 30 sample points (using linear interpolation between adjacent values in the original to approximate required samples that fell "in the cracks"). I did not try to interpolate across stretches where the pitch-tracker failed to return a value, but just left a nominal value of 0 in the result in those cases.
The result of this procedure was a matrix of 7,992 rows (syllables) and 30 columns (f0 sample sequences). A corresponding text file is available as all.f01 -- we can read it into Octave or Matlab as follows:
f0data = load('-ascii', 'all.f01');
Now we want to eliminate rows with zeros in them -- it would be better to interpolate across the regions where pitch was not tracked, but it's simpler to leave this out for now.
zerorows = (min(f0data')==0); f0data1 = f0data(~zerorows,:);
nvals=length(f0data1(:,1))
There are 7,101 rows without zero values, so we've lost 7992-7101=891 syllables, which is too bad but tolerable for now.
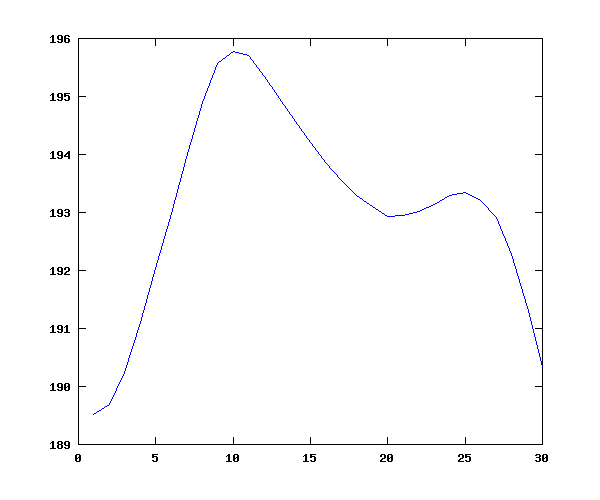
Now let's plot the overall mean (syllable-level) contour, which (plausibly) shows lower values near the consonantal margine, and an overall down-trend, all within a fairly small compass of about 6 hz in 190, or about 3%:
f0means = mean(f0data1); plot(f0means);
Another matrix, this one 7,992 by 10, contains indicator variables for the 7,992 syllables (presented in text form in all_ind.f0). The columns are:
% 1 speaker
% 2 statement(0) or question(1)
% 3 sentence has focus? 0=no, 1=yes
% 4 focus location (if any): syllable 1, 5 or 8
% 5 tone category of the focused syllable (if any) 1, 2, 3, or 4 % 6 sentence "group" (1 to 8) % 7 location of the current syllable within the phrase (1 to 8) % 8 frame number of the first f0 sample in the original sentence contour % 9 frame number of the last f0 sample in the original sentence contour
% 10 tone category of the current syllable (1 to 5)f0inds = load('-ascii', 'all_ind.f0'); f0inds1 = f0inds(~zerorows,:);
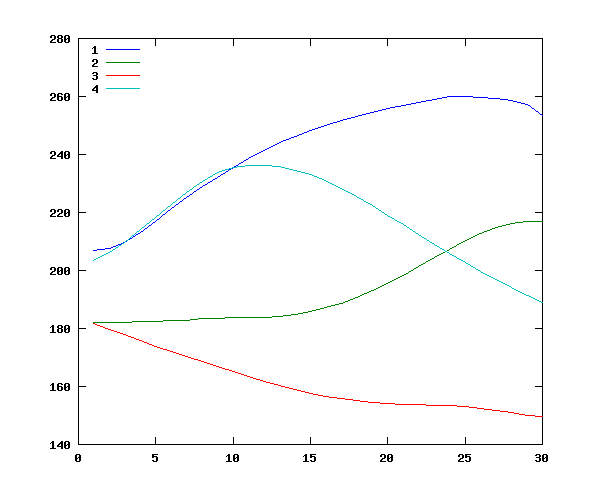
We can use this matrix of indicator variables to check a few main effects. For instance, we can look at the overall mean contours for the four tones:
tonemeans=zeros(4, 30);
for tone=1:4
tonemeans(tone,:) = mean(f0data1(f0inds1(:,10)==tone,:));
end
plot(tonemeans')
legend(' 1',' 2',' 3',' 4','location','northwest')
This gives plausible overall values for tone 1 ("high"), tone 2 ("rising"), tone 3 ("low"), and tone 4 ("falling") -- especially since the distribution of contexts is non-orthogonal:
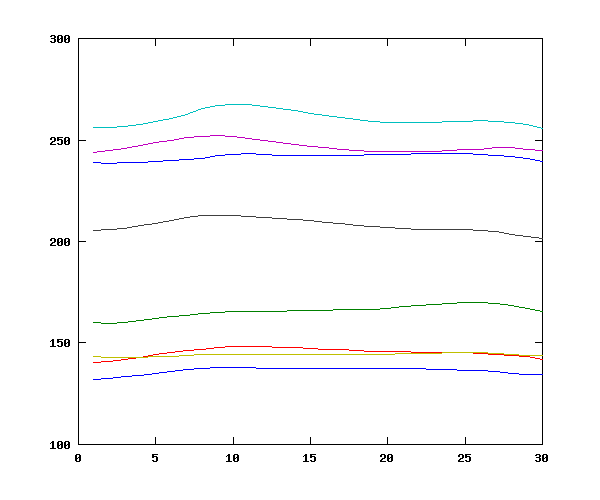
Now we can do the same thing for the main effect of speaker:
speakermeans= zeros(8,30);
for speaker=1:8
speakermeans(speaker,:) = mean(f0data1(f0inds1(:,1)==speaker,:));
end
mean(speakermeans')
ans = 241.67 165.70 145.40 260.69 246.93 144.19 207.97 136.32
plot(speakermeans');
Again, this gives plausible results, consistent with the presence of four male and four female speakers:
Let's examine the interaction between speaker and tone, comparing tone 1 and tone 3 for the speaker with the highest mean f0 (speaker 4) and the lower mean f0 (speaker 8). This yields the plausible result that speaker 8's "high" tone is lower than speaker 4's "low" tone, confirming the need for some normalization:
speakermeans= zeros(8,30);
for speaker=1:8
speakermeans(speaker,:) = mean(f0data1(f0inds1(:,1)==speaker,:));
end
stm=zeros(8,30);
stm(1,:) = mean(f0data1((f0inds1(:,1)==4) & (f0inds1(:,10)==1),:));
stm(2,:) = mean(f0data1((f0inds1(:,1)==4) & (f0inds1(:,10)==3),:));
stm(3,:) = mean(f0data1((f0inds1(:,1)==8) & (f0inds1(:,10)==1),:));
stm(4,:) = mean(f0data1((f0inds1(:,1)==8) & (f0inds1(:,10)==3),:));
yrange = [min(min(stm))-10 max(max(stm))+10];
figure(1); newplot();
subplot(1,2,1); plot(stm(1:2,:)'); title('Speaker 4'); ylim(yrange);
subplot(1,2,2); plot(stm(3:4,:)'); title('Speaker 8'); ylim(yrange);

As is often the case, there's the question of what the appropriate "graph paper" is. Should we normalize by subtracting a constant value? or by using a log transform, which would turn constant ratios into constant differences? One way to examine this is to look at the relationships between corresponding portions of two different speakers mean time-functions for various tones. That is, we plot the first value for speaker 8's average tone 1 against the first value for speaker 4's average tone 1, the second value against the second value, and so on. This gives us something like this:
stm(5,:) = mean(f0data1((f0inds1(:,1)==4) & (f0inds1(:,10)==2),:));
stm(6,:) = mean(f0data1((f0inds1(:,1)==4) & (f0inds1(:,10)==4),:));
stm(7,:) = mean(f0data1((f0inds1(:,1)==8) & (f0inds1(:,10)==2),:));
stm(8,:) = mean(f0data1((f0inds1(:,1)==8) & (f0inds1(:,10)==4),:));
figure(2); subplot(1,1,1); newplot();
plot(stm(1,:),stm(3,:),'b*',stm(2,:),stm(4,:),'ro', stm(5,:),stm(7,:),'gx', stm(6,:),stm(8,:),'k+',yrange,yrange,'k-');
xlim(yrange); ylim(yrange);
xlabel('Speaker 4'); ylabel('Speaker 8')
legend('Tone 1','Tone 3','Tone 2','Tone 4','location','northwest')
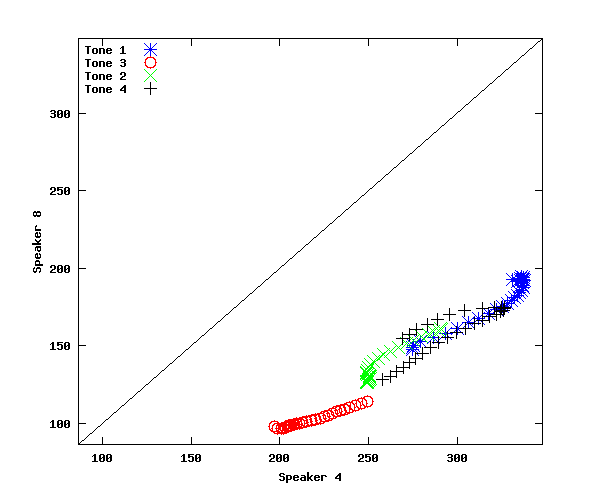
In the plot we've just made, the points are not parallel to y=x (as they would be if there was on average a constant additive difference between speakers), but neither do they fall along a line of constant slope and 0 intercept (as they would if there was on average a constant multiplicative difference between speakers).
We can check for this more directly by plotting one speaker's values against their ratio to corresponding values for another speaker:
figure(3); subplot(1,1,1); newplot(); plot(stm(1,:),stm(1,:)./stm(3,:),'b*',stm(2,:),stm(2,:)./stm(4,:),'ro', stm(5,:),stm(5,:)./stm(7,:),'gx', ...
stm(6,:),stm(6,:)./stm(8,:),'k+'); xlabel('Speaker 4'); ylabel('Speaker 4 / Speaker 8'); legend('Tone 1','Tone 3','Tone 2','Tone 4','location','northwest')

In that plot, you can see that the ratio is not constant, but rather falls over quite a wide range (roughly 2.15 to 1.75) as the basic pitch increases. This suggests an additive component in the relationship, which would cause the ratio to shrink in this way.
On the other hand, a direct check of an additive relationship also fails badly:
figure(4); subplot(1,1,1); newplot(); plot(stm(1,:),stm(1,:)-stm(3,:),'b*',stm(2,:),stm(2,:)-stm(4,:),'ro', stm(5,:),stm(5,:)-stm(7,:),'gx', ...
stm(6,:),stm(6,:)-stm(8,:),'k+'); xlabel('Speaker 4'); ylabel('Speaker 4 - Speaker 8'); legend('Tone 1','Tone 3','Tone 2','Tone 4','location','northwest')
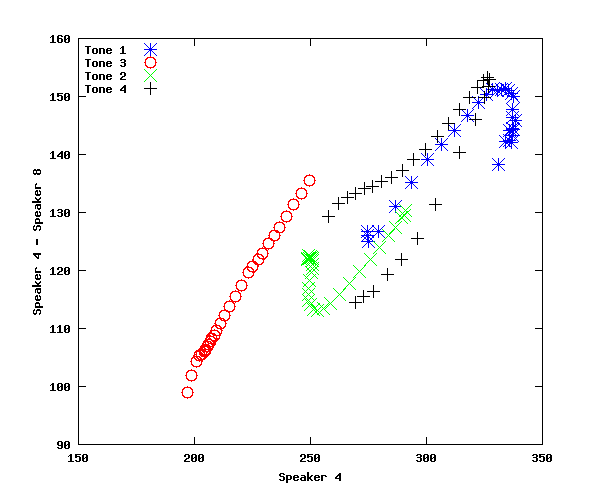
Again, the difference is not constant, but increases with increasing f0 -- suggesting a multiplicative component in the relationship.
How to model speaker-related pitch-range effects.
We've just seen that neither an additive model nor a multiplicative one is likely to be correct (which is not to say that such models would not fit quite well, as in the case of tree-weight data...).
Would the problem be fixed by using a semitone scale? You could try it...
N.B. A semitone is a 1/12 of an octave, and an octave is a ratio of 2/1, so a semitone is a ratio of
2^(1/12)
In order to turn a value V in hz to a value in semitones, we have to pick a base value B and then calculate x such that
V/B = (2^(1/12))^x
Thus x = (log(V)-log(B))/log(2^(1/12))
What if each speaker's f0 values were a linear function of some underlying scale, with possibly different slope and intercept? That this could yield qualitatively similar results is shown below. Could such a model fit quantitatively? What would it mean?
Vhat = .01:.01:1.0; NN = length(Vhat);
V1 = 50*Vhat + 50; V2 = 100*Vhat + 150;
yrange = [0 max(V2)+10];
figure(1); subplot(2,2,1);
plot(1:NN,V1,'bx',1:NN,V2,'ro');
xlabel('Time'); ylabel('Pitch'); legend('V1','V2','location','northwest');
subplot(2,2,2); plot(V2,V1,'rx',yrange,yrange,'k-');
xlim(yrange); ylim(yrange);
xlabel('V2'); ylabel('V1');
subplot(2,2,3); plot(V2, V2./V1, 'rx');
xlabel('V2');ylabel('V2./V1');
subplot(2,2,4); plot(V2,V2-V1,'b*');
xlabel('V2');ylabel('V2-V1');

What about z-score normalization? (That is, representing each speaker's pitches in terms of standard deviations above or below that speaker's mean.) What does this predict qualitatively about these scaling relationships? What happens if you fit such a model quantitatively in this case?
Funtional Principal Components
Now we can try the method for finding "eigencontours" (or "functional principal components") used in the Aston et al. paper, which is to look at the eigenstructure of the covariance matrix. We will find that the five eigenvectors with the largest eigenvalues look quite a bit like the first few orthogonal polynomials in the last exercise:
f0cov = cov(f0data1);
[V L] = eig(f0cov);
LL = diag(L);
% Note that eigenvectors are in columns of V
% with eigenvalues ordered from smallest to largest
basis5 = V(:,30:-1:26)';
figure(1); plot(basis5'); title('Five eigenvectors')
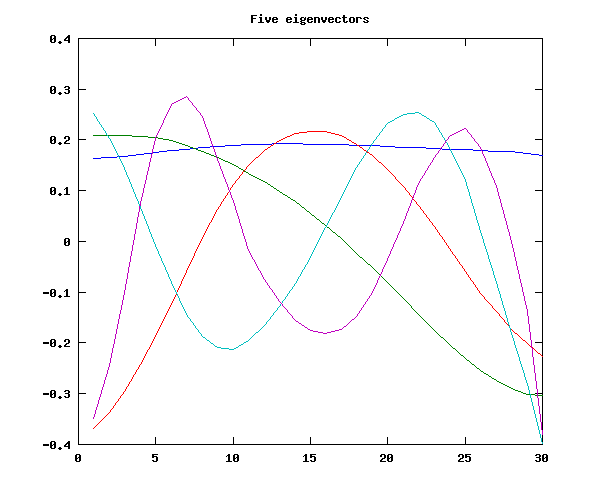
We will find that these five eigenvectors do quite a good job of approximating (a sample of) the original contours:
for n=1:6 coeffs = basis5'\f0sample(n,:)'; synth = basis5'*coeffs; subplot(2,3,n); plot(1:30,f0sample(n,:),'b',1:30,synth,'r'); end

Four components do nearly as good a job; three is a bit worse, and two is marginal.
Again, some experiments for the intrepid:
- Use the results of FPCA to classify tones, focus status, etc. (e.g. via linear discriminant analysis)
- Compare COP parameters in the same tasks
- Try variants of FPCA that don't require time-normalization (as discussed e.g. in Pantelis Hadjipantelis et al., Pantelis Z., "Unifying amplitude and phase analysis: A compositional data approach to functional multivariate mixed-effects modeling of Mandarin Chinese." Journal of the American Statistical Association2015).
The last experiment requires the original data -- let me know if you want it -- but I'd suggest starting with fake data, as in the first segment above, in order to verify that your method can work when the "truth" is known.