
| Home | <- Week 5-6 | Week 8-> |
install.packages("gtools")
When working with categorical data (vs Continuous or Count), the normal distribution is no longer appropriate one for our purposes. Rather, tests for proportions are based in the binomial distribution. Where the normal distribution gives you the probability of getting a value within a certain range, the binomial distribution gives you the point probabilities of getting x sucessesful trials out of N trials given a probability p of success. So, if you were rolling fair, 6 sided dice 50 times, the probability of rolling a five 10 times is 11.6%, as given by
dbinom(x=10,size = 50,prob = 1/6)
Here's a plot of all the point probabilities, from rolling 0 fives to rolling 50 fives:

The binomial distribution is apparently well approximated by a normal distribution with &mu = Np and a σ2 = Np(1-p), but only when Np > 5 and N-Np > 5 (I believe). It's this normal approximation (actually χ2) that underlies prop.test(), which we'll talk about soon. binom.test() is based on the binomial distribution, and should be used instead when possible, but it can only be used for one-sample type problems (i.e. it can't be used to see if two proportions are significantly different).
You can add the normal approximation to the plot above with this code.
N <- 50; p <- 1/6
mu<-N*p
s<-sqrt(mu*(1-p))
curve(dnorm(x,mean = mu, sd = s),add = T, col = "red")
If you have one proportion that you would like to test whether it is significantly different from some a priori assumption, you can use prop.test() or binom.test(), much like a one-sample t-test for continuous data. I think the R help page for binom.test() provides a good example of where you may have an a priori assumption about proportions.
Say you were studying genetic inheritance, and your theory predicted that 3/4 of the offspring of two pea plants would be giants, and 1/4 would be dwarves. After breeding them, you end up with 682 giants, and 243 dwarves, for a total of 925 offspring. So, 73.7% of the offspring were giants, but is that significantly different from 75%? To use prop.test() or binom.test(), we need to give them the number of "success" (number of giants here), the total number of trials (the number of offspring here) and the expected probability. As a rule, you can't do tests on categorical data with just the proportions, since the confidence interval of those proportions depends upon the sample size. Also keep in mind that binom.test() is the preferred test here.
prop.test(682,n=925,p=3/4)
binom.test(682,n=925,p=3/4)
So, we can see that the results of the breeding are not inconsistent with the hypothesis that 3/4 of the offspring would be giants. Notice that prop.test() used the Yates continuity correction by default. This is really important if either the expected successes or failures is < 5, but otherwise it has an effect of producing wider confidence intervals. Here, it would be ok to pass the argument correct = F to prop.test().
You can also use prop.test() to compare two proportions to see if they are significantly different. This kind of test is different in nature from testing whether the distribution of success vs. failures is independent from which group theY are in (a chi-squared test), but the result is about the same. For this kind of data, just use a chi-squared test (to be discussed). I'm just mentioning it here, because we'll look at pairwise.prop.test() later on.
The Chi-Square test is the most commonly used test for the independence of the distribution of some categorical variable into some groups. Say you have some variable which can take categorical values x, y, and z, and you're interested in how groups A, B, and C behave in regards to this variable. Your observations could be fit into a table like this, where xA is the number of x observations for group A, xTot is the total number of x observations, and TotA is the total number of A observations, and so on.
| A | B | C | Total | |
|---|---|---|---|---|
| x | xA | xB | xC | xTot |
| y | yA | yB | yC | yTot |
| y | zA | zB | zC | zTot |
| Total | TotA | TotB | TotC | Total |
You can calculate how many observations you would see in each cell if the distribution of the categorical variable was independent across groups, with the following formula in each cell:
| A | B | C | Total | |
|---|---|---|---|---|
| x | (xTot*TotA)/Total | (xTot*TotB)/Total | (xTot*TotC)/Total | xTot |
| y | (yTot*TotA)/Total | (yTot*TotB)/Total | (yTot*TotC)/Total | yTot |
| y | (zTot*TotA)/Total | (zTot*TotB)/Total | (ZTot*TotC)/Total | zTot |
| Total | TotA | TotB | TotC | Total |
So, where the first table is the Observed and the second table is Expected, you can calculate a χ2 value for this data with Σ(Observed-Expected)/Expected, where you are summing over all cells. Whether a chi-square value is significant depends on the number of degrees of freedom in the data, which is (nrows-1)*(ncols-1). A significant Chi-square value tells us that the distribution of variable observations is not independant across groups.
To illustrate, we'll use some ING data collected from South Philadelphians. The variable of interest here is whether speakers said -ing (with a velar nasal) or -in (with an apical nasal). The groups across which we'll look at this first are following segments. Are -ing and -in distributed independently across tokens with a following apical segment vs a following velar segment?
fol<-rbind(In=c(181,11),Ing=c(137,26))
colnames(fol)<-c("apical","velar")
fol
There's the data table for in vs ing across these groups. To see the proportions across groups, we can use prop.table(), which takes a matrix or table as its first argument, and then 1 (for rowwise proportions) or 2 (for columnwise proportions).
prop.table(fol,2)
The proportions are definitely different, but the Chi-square test will tell us if they are significantly so. None of the expected values will be < 5, so we'll do it without the Yates correction.
chisq.test(fol,correct = F)
So, with a very small p-value, the distribution of in and ing across these two groups is significantly different. Since this was just a 2X2 table, the interpretation of the significant chi-square result is very clear. in and ing are distributed signficantly differently with respect to the following segment. However, ING data was collected in more contexts than those with following apicals and velars. Those contexts could also be included in a chi-square test.
ing <- read.csv("http://www.ling.upenn.edu/~joseff/rstudy/data/ing2.csv")
fol1<-table(ing$DepVar, ing$Following.Seg)
fol1
prop.table(fol1,2)
folchi<-chisq.test(fol1)
folchi
Again, we get a significant chi-square value, but this time its interpretation is a little less clear. All we can say as a result of this is that variants of the ING variable are not independently distributed across contexts. Although we can't be exactly sure which groups have skewed distributions, we could try looking at the table from which χ2 was calculated.
O<-folchi$observed
E<-folchi$expected
(O-E)^2/E
By comparing the χ2 table to the proportional table, we can see that a higher than expected rate of /in/ for following apicals, and a higher than expected rate of /ing/ for velars and palatals contributed the most to χ2.
We could also do a pairwise proportion test, much like the pairwise t-test, which would compare every group's proportion, correcting for the fact multiple tests are being done.
##we need to transpose fol1 with t()
##this takes a matrix with
##a column of successes and a column of failures
pairwise.prop.test(t(fol1))
It looks like palatals and velars are significantly different from apicals, but no other group difference is significant.
One thing to keep in mind, especially with this data, is that we may have too finely grained distinctions between groups than there are. That is, following consonants which are articulated with the tongue may be the only contexts which have effects, and of those, the important distinction is whether they are articulated with the tongue blade, or with the tongue body. We might try collapsing categories into Apical, Posterior, and Other.
fol2<-cbind( other=rowSums(fol1[,c("0","labial","vowel")]),
apical = fol1[,"apical"],
posterior = rowSums(fol1[,c("palatal","velar")]))
fol2
Now we can look at some of the same diagnostics.
prop.table(fol2,2)
folchi2<-chisq.test(fol2)
E<-folchi2$expected;O<-folchi2$observed
(O-E)^2/E
pairwise.prop.test(t(fol2))
Before we go on to modeling, we should create a new factor in ing for use later.
ing$Tongue<-"other"
ing[ing$Following.Seg %in% c("velar","palatal"),]$Tongue <- "posterior"
ing[ing$Following.Seg =="apical",]$Tongue <- "apical"
ing$Tongue<-as.factor(ing$Tongue)
ing$Tongue<-relevel(ing$Tongue,"other")
These methods with contingency tables are alright for looking at the effect of one predictor on one response variable, but typically you'll want to look at multiple predictors' effects on a response. For this purpose, we'll use a logistic regression, which is one of a number of models called generalized linear models, or GLMs.
The idea behind a logisic regression is nearly the same as behind a linear regression. The difference is that the fitted values it returns should be probabilities success. However, we wouldn't want to fit some kind of linear model against raw probabilities. Probabilites cannot be greater than 1, or less than 0, and a linear model fit against raw probabilities could produce fitted values outside this range. What's more, when a categorical variable changes across a continuous variable, it does so with an S shape, like the logistic curve below.
On a raw proportional scale, differences between proportions isn't additive. That is, the difference between 50% and 55% is not the same as the difference between 90% and 95%. For this reason, a logistic regression uses a logistic "link," returning a linear function of the following form:
On a logit scale, changes in proportion look like this:

On this scale, the values of the coefficients are in log-odds (p/(1-p) is the odds, and we take the log of it). These can be pretty easy to interpret with some experience. You can see how they compare to probabilities with this code:
library(gtools)
p<-c(0.99,0.95,0.9,0.8,0.7,0.6,0.5,0.4,0.3,0.2,0.1,0.05,0.01)
cbind(p,logit(p))
The most important thing to notice is that logit(0.5)=0. This means that if you have a predictor that gets back a value of 0, this means that the response has a 50% probability of a success given this predictor. Since we're looking at binomial variables here, this predictor effectively has no effect on the response variable, so the 0 value is very meaningful. Likewise, a negative coefficient indicates a predictor disfavoring success, and a positive coefficient indicates favoring success.
glm() is the function for doing logistic regressions in R. It can take a few different kinds of arguments. First, we'll give it a table of successes and failures.
gttable<-table(ing$DepVar,ing$GramStatus,ing$Tongue)
ing.obs<-rbind(t(gttable[,,"other"]),t(gttable[,,"apical"]),t(gttable[,,"posterior"]))
ing.tbl<-expand.grid(Tongue = levels(ing$Tongue),GramStatus = levels(ing$GramStatus))
ing.tbl
ing.obs
ing.tbl is a table of cross conditions of Grammatical Status, and Tongue articulator. ing.obs is a table of observations for each condition. Let's do a regression using gramatical status and tongue articulator as predictors. First, we'll want to change the default contrasts for grammatical status to sum contrasts, since we don't know what the no-treatment condition is. We can use a script I wrote for this to make it easy.
source("http://www.ling.upenn.edu/~joseff/scripts/recontrast.R")
ing.tbl$GramStatus <- recontrast(ing.tbl$GramStatus)
##now for the regression
ing.mod<-glm(ing.obs~ing.tbl$GramStatus+ing.tbl$Tongue,family = binomial)
summary(ing.mod)
The output of glm() isn't so different from what we've seen with linear models. You should be cautious if the residuals get too high, because that indicates that some cells are poorly fitted. Otherwise, the regression coefficients are pretty straight forward:
Now, this wasn't the easiest way to fit a logistic regression for this data. However, if you have data of, say, looking times to target vs distractor, you could structure the data so that every row is a trial, with a column for milliseconds looking at target and a column for miliseconds looking at distractor, with a dataframe of the predictors you have for each trial. You could then fit the model exactly like we just did here.
For this data, however, it's easiest to look at it as just a hit or miss per trial, which is just as easy to fit.
ing<-recontrast(ing)
ing$Tongue<-recontrast(ing$Tongue,type = "treatment")
ing.mod<-glm(DepVar~GramStatus+Tongue,data = ing, family = binomial)
summary(ing.mod)
You'll notice that the signs have changed on the coefficients, but that's just because in this model what counted as a success and a failure was reveresed from the previous model. Everything else is the same though, so all you need to keep straight is which probability we're modeling.
Let's calculate the effect for the "thing" grammatical class, and sort the grammatical classes from most "in" favoring to most "ing" favoring.
thing<-sum(ing.mod$coef[2:7])*-1
sort(c(ing.mod$coef[2:7],thing))
Here's the very well known grammatical effect on ING variation, which goes all the way back to when the English participial morpheme was "inde" and the gerundive morpheme was "inge" (Labov 1989, Houston 1985).
The analysis of deviance table is also rather important for evaluating logistic models.
anova(ing.mod, test = "Chisq")
Every row in the table tells us how much every term reduces deviance in the model, and the chi-square test tells us if it is significant. you need to pass test = "Chisq" to anova() in order to get these significance values. Again, the order of predictors will affect whether others are significant in the analysis of deviance.
In the grand tradition of sociolinguistics, let's do a stepwise regression!
ing.mod1<-step(glm(DepVar~1,data = ing,family = binomial), DepVar~Style+GramStatus+Sex+Age+Tongue)
summary(ing.mod1)
anova(ing.mod1,test = "Chisq")
It may be the case that you will have some data that has a polynomial relationship to the response. This can be true of linear regressions as well, but I have some good data with this kind of relationship with categorical data.
donner<-read.csv("http://www.ling.upenn.edu/~joseff/rstudy/data/donner.csv")
This is a data set for the Donner Party. We can fit a logistic regression of survival against age easilly enough.
don.mod<-glm(NFATE~AGE,data = donner,family =binomial)
##more like family = delicious, amiright?
summary(don.mod)
Not to surprisingly, as age increases, probability of survival decreases. But this isn't necessarily the best model of the data. We can look at the way survival changes over age by adding a smoothing line to a plot.
plot(donner$AGE,donner$NFATE)
lines(lowess(donner$AGE,donner$NFATE))

It looks like younger people and older people are more likely to die than people in between. We can fit this polynomial relationship directly. We'll use age, and the square of age as predictors. To pass the square of AGE to glm, we'll use the I() operator in the formula. When you used I(), it essentially means "interpret this as the actual mathematical function, not a model formula".
don.mod1<-glm(NFATE~AGE+I(AGE^2),data = donner, family = binomial)
summary(don.mod1)
Now, this output is a little more difficult to immediately interpret, because this is formula for a second order equation. What we can see right off the bat is that the sign of the second order term is singificantly negative, which means that younger and older people are significantly more likely to die than people in the middle.
The easiest way to intepret the output of this equation is to plot it.
pred<-expand.grid(AGE= 1:65)
pred$Fit<-predict(don.mod1,newdata = pred,type = "resp")
plot(donner$AGE,donner$NFATE)
lines(pred$AGE,pred$Fit)

We can also solve for the peak age of survival, by taking the first derivative of the equation, and solving for 0.
don.mod1$coef
peak.age<- -don.mod1$coef[2]/(2*don.mod1$coef[3])
abline(v = peak.age)
peak.age
inv.logit(sum(c(1,peak.age,peak.age^2)*don.mod1$coef))
Which comes to about 17.5 year olds having about 68% probability of survival, and then it's downhill on either side of them.
Every model we've fitted so far has been strictly additive. That is, PredictorX has an effect, and PredictorY has an effect, and they are simply added. But maybe X and Y can have an interaction effect as well. Typically, you'll want to see if membership to some group has an interaction effect with some other grouping, or along some continuous variable.
For example, something we might look at in sociolinguistics might be whether Gender interacts with socioeconomic class, or with stylistic shifting. It is probable, depending on the variable being studied, that men will style shift differently, but maybe not divergently, from women. Or, it may be the case that people in different experimental groups might have different sensitivities to some variable you are controlling for.
I happen to have some good data for looking at interactions involving the effect of frequency and grammatical class on the rate of -t/d deletion in English.
In English, word final consonant clusters, especially those with a final /t/ or /d/ are likely to be simplified by deleting the final /t/ or /d/. There are at least 4 grammatical classes which are affected by this simplification:
It's been noted for a long time that there is a grammatical effect on -t/d deletion. The order of grammatical classes in order of least to most deletion is Regular < Irregular < Monomorpheme < not-contraction. Recently, more attention has begun to be paid to the effect of frequency on deletion.
Here is a subset of a data set drawn from the Buckeye corpus, with every token coded for deletion, grammatical class, and log(frequency) in the corpus.
sbuck<-read.csv("http://www.ling.upenn.edu/~joseff/rstudy/data/sbuck.csv")
sbuck$Gram<-relevel(sbuck$Gram,"Past")
sbuck<-recontrast(sbuck)
summary(sbuck)
So, let's fit a regression against log(frequency).
bmod<-glm(DepVar~Log_Freq, data = sbuck,family = binomial)
summary(bmod)
So as log(frequency) increases by 1, the log-odds of having a /t/ or /d/ decreases by 0.30, and a word with log(frequency) = 0, or a frequency of 1 will have log-odds of having a /t/ of 1.37. Let's plot this result:
plot(sbuck$Log_Freq, sbuck$DepVar,type = "n")
pred<-expand.grid(Log_Freq = seq(min(sbuck$Log_Freq),max(sbuck$Log_Freq),length = 50))
pred$fit<-predict(bmod,newdata = pred, type = "response")
lines(pred$Log_Freq, pred$fit)
Now, membership in a grammatical class may have an additive effect on deletion, meaning that each grammatical class may have a different intercept, but parallel slopes over frequency. Let's fit that model.
bmod1<-glm(DepVar~Gram+Log_Freq, data = sbuck,family = binomial)
summary(bmod1)
anova(bmod1,test = "Chisq")

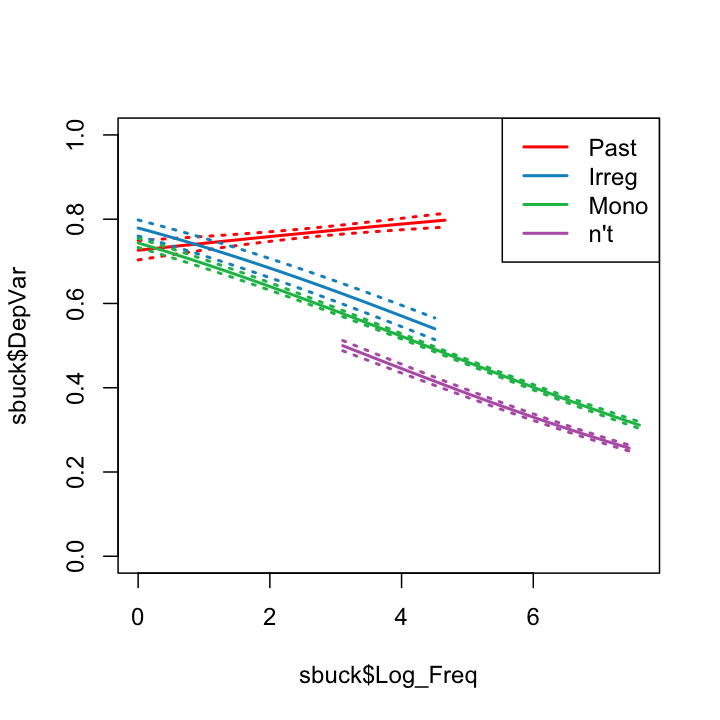
But the effect of frequeny might not be uniform across grammatical classes. To test this, we'll an interaction effect.
bmod2<-glm(DepVar~Gram*Log_Freq, data = sbuck,family = binomial)
summary(bmod2)
What this returns is a function, essentially of the form
To see if the interaction really does significantly improve the fit of the model, we should look at the analysis of deviance table:
anova(bmod2,test = "Chisq")

puck<-sbuck[sbuck$Gram != "Past",]
drop.levels(puck)->puck
recontrast(puck)->puck
bmod3<-glm(DepVar~Gram*Log_Freq, data = puck,family = binomial)
summary(bmod3)
anova(bmod3,test = "Chisq")
sbuck$Gram2 <- "other"
sbuck[sbuck$Gram == "Past",]$Gram2<-"past"
as.factor(sbuck$Gram2)->sbuck$Gram2
bmod4<-glm(DepVar~Gram+Log_Freq:Gram2,data = sbuck,family = binomial)
summary(bmod4)
don.mod2<-glm(NFATE~GENDER*AGE+GENDER*I(AGE^2),data = donner, family = binomial)
summary(don.mod2)
f.age <- -don.mod2$coef[3]/(2*don.mod2$coef[4])
m.age <- -(don.mod2$coef[3]+don.mod2$coef[5])/(2*(don.mod2$coef[4]+don.mod2$coef[6]))
f.age
m.age