Summer 2010 — R: Summarization and Aggregation

<- R: Basics

Home

R: Functions->

Intro

Basics

table()
tapply()

Split Apply Combine
transform() and summarize()

transform()
summarize()

Arbitrary Functions

Repetition Example
Normalization Example
Models example

Intro

Raw data is usually useful in its static state. Therefore, it's important to have a good toolset for summarizing and aggregating data.

Basics

There are quite a few good summarization functions in base R. The simplest are table() and tapply(). I'll be demonstrating their use with a dataset of recorded telephone numbers, here.

Briefly, I read 93 strings of 7 numbers formatted as telephone numbers (e.g. 123-4567). Begin and End contain the begin and end time of the number in the recording in seconds. Duration is End-Begin. Label is the number which was read, Num is an ID for each number sequence, and Pos represents the position in the number sequence.

The data is tab delimited, so we can load it with the following code.

dur <- read.delim("http://www.ling.upenn.edu/~joseff/rstudy/data/Joe.Durr1.txt")

table()

The table() function creates a table of counts of observations of values in factors you pass to it.

## How many of each number?
table(dur$Label)

##How many of each position?
table(dur$Pos)

##How many of each number in each position?
table(dur$Label, dur$Pos)
##Add some meaningful names to that table?
table(Label = dur$Label, Position = dur$Pos)

To get proportions in each cell of a table, wrap the table() function in prop.table(). If you pass 1 to the margin argument, it will calculate proportions row-wise, and if you pass 2, it will calculate proportions column-wise. If you don't pass any value to the margin argument, it will calculate grand proportions.

table(Label = dur$Label, Position = dur$Pos)

## Row-wise
prop.table(table(Label = dur$Label, Position = dur$Pos),1)

## Column-wise
prop.table(table(Label = dur$Label, Position = dur$Pos),2)

## Grand proporiton
prop.table(table(Label = dur$Label, Position = dur$Pos))

tapply()

The tapply() function will "apply" an arbitrary function to subsets of data. I'll be calculating means over the log of duration, since duration tends to be lognormally distributed.

## Geometric mean duration by number
exp(tapply(log(dur$Duration), dur$Label, mean))

## Median duration by number
tapply(dur$Duration, dur$Label, median)

## Total seconds spent on each number
tapply(dur$Duration, dur$Label, sum)

The nifty thing about tapply() is that you can also apply the function to cross-classified data.

## Geometric mean duration by number by position
exp(tapply(log(dur$Duration), list(dur$Label, dur$Pos), mean))

## Sum of durations by number by position
tapply(dur$Duration, list(dur$Label, dur$Pos), sum)

Split Apply Combine

Frequently, you'll want to do something a bit more complex than tapply() can offer you, or you might want the output formatted a little differently. For these purposes, I'd suggest using the plyr package. The plyr website is here: http://had.co.nz/plyr/. I would highly recommend checking it out, and reading through the documentation[PDF].

As the plyr documentation discusses, when you want to aggregate or summarize data, what you really want to do is split the data up into meaningful subsets, apply the same function or operation to every subset, then combine the results of every application into a single output. There already exist a bunch of functions in base R for this approach to aggregation (like aggregate()). What plyr offers is consistent naming conventions and syntax for the various approaches.

The core of plyr functionality is its series of __ply() functions, which all take the form of xyply(), where x stands for the input data structure, and y stands for the desired output data structure. The most common inputs and outputs are:

	Structure
a:	array
d:	data frame
l:	list

Most of the data structures we work with are data frames, and usually we'll want to keep working with data frames, so ddply() is the plyr function we'll use the most.

ddply() takes three main arguments.

data: The data frame containing the data.
variables: The variables to split the data frame up by.
fun: The function to apply to the data frame subsets.

The simplest function we can apply to an entire data frame and get meaningful results is nrow(). Let's apply nrow() to subsets defined by Label, Pos, and Label and Pos. d*ply() functions have a few different ways of specifiying the variables you want to split by. They're all equivalent, so choose the one that you feel most comfortable with (see documentation for details).

## Split by Label
ddply(dur, .(Label), nrow)

## Split by Pos
ddply(dur, .(Pos), nrow)

## Split by label and Pos
ddply(dur, .(Label, Pos), nrow)

You can also create variables on the fly to split the data frame by. For example, I could split the data on various binnings of Duration

## cut() Duration into 10 bins
ddply(dur, .(DurBins = cut(Duration, 10)), nrow)

## round() Duration to the nearest 1/10th second
ddply(dur, .(DurBins = round(Duration, 1)), nrow)

transform() and summarize()

Some other useful out-of-the-box functions to use with ddply() are transform() and summarize(). These functions operate over entire data frames. We can see how they work by applying them to a manual subset of the duration data.

transform()

## Subset of just "zero" in first position
sub01 <- subset(dur, Label == 0 & Pos == 1)

## transform duration to log centered
sub01 <- transform(sub01, Dur_center = log(Duration) - mean(log(Duration)))

After using transform(), sub01 now has a new column called Dur_center which has values which are the log of Duration minus the mean of the log of Duration.

What if you wanted to apply this transformation to every subset of the data defined by unique combinations of Label and Pos? One way you could do it is to write a loop that takes every unique subset, applies the transformation, then pastes it all together again at the end. Or, you could use ddply() as follows.

## Log center every subset defined by Label:Duration
dur <- ddply(dur, .(Label,Pos), transform, Dur_center = log(Duration) - mean(log(Duration)))

Having applied this transformation, we could see how atypical a given recitation of a number in a given position is compared to some other variable (ideally, we'd use z-scores, or residuals for this). For example, how did my speech rate vary over the length of the recording?

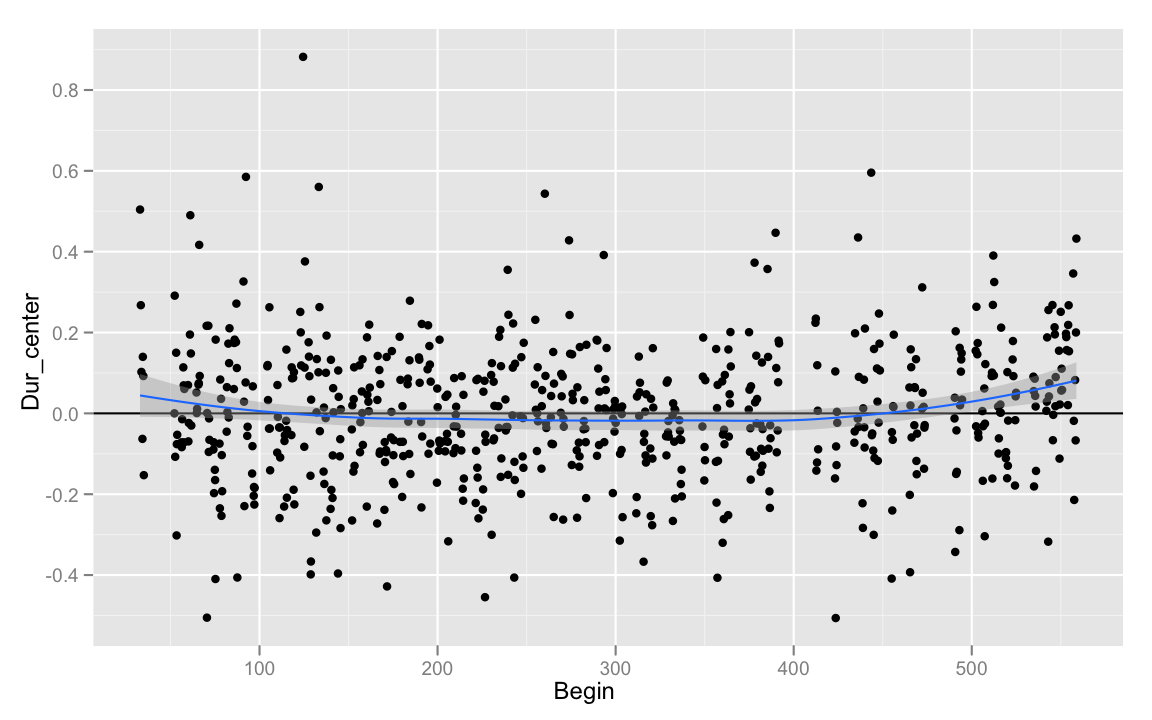
summarize()

summarize() is actually a function from the plyr package. Its behavior is somewhat different from transform(). First, let's look at what it does with the same subset of the data as above.

## summarise dur
summarise(sub01, Dur_mean = mean(Duration), Dur_sum = sum(Duration), Dumb = mean(end) - mean(Begin))

Rather than returning the entire original data frame with additional columns, summarize() returns only the derived columns. So, let's apply the same summarization to every subset of the data with ddply().

dur_summary <- ddply(dur, .(Label, Pos), summarize, Dur_mean = mean(Duration), Dur_sum = sum(Duration), Dumb = mean(end) - mean(Begin))

Arbitrary Functions

Repetition Example

You can also write your own arbitrary functions that take data frames as arguments, and pass them as arguments to ddply().

What if I wanted to test the hypothesis that if I read a number sequence where one of the numbers is immediately repeated (e.g. 123-4566), the second repetition of the number will be shorter. Let's write a special function to be passed to ddply() to code the data properly.

codeRepeat <- function(df){
  ## Make sure the dataframe is properly ordered
  df <- df[order(df$Pos),]
  
  ## If the difference between two adjacent labels
  ## is 0, they are the same label. The first label
  ## cannot have been a repeat. 
  df <- transform(df, Repeat = c(NA, diff(df$Label) == 0))
	
  return(df)
}

Now, pass the codeRepeat() function to ddply. We want to apply codeRepeat() to every unique sequence of numbers.

## apply the codeRepeat() function for every
## string of numbers, identified by Num
dur <- ddply(dur, .(Num), codeRepeat)

Now that we've got the data coded, it's only a matter of running the proper analysis.

mod <- lm(log(Duration) ~ factor(Pos)*factor(Label)*Repeat, data = dur)
anova(mod)

Florian Schwarz had an excellent suggestion for doing this same analysis quickly with data that is coded as a factor. If Label had coded as "one", "two", etc, we could not have used diff() in the codeRepeat() function the same way. However, we could easilly reformat the factor to numeric indices with as.numeric(), then used codeRepeat() in the same way.

Normalization Example

I wrote this function to normalize formant data according to the ANAE method (there is also an ANAE normalization function in the vowels R package).

AnaeNormalize <- function(df, G = 6.896874, formants = c("F1","F2")){
  m <- length(formants)
  n <- nrow(df)
  
  S <-  sum( log(df[ , formants]) ) / (m*n)
  
  F <- exp(G - S)
  
  norm_formants <- paste(formants, "norm", sep = "_")
  
  for(i in seq(along = formants)){
    df[[ norm_formants[i] ]] <- df[[ formants[i] ]] * F  
  }
  
  return(df)
}

We can test this function out using some data from the SLAAP project's NORM sample data sets.

## read in the data
samp <- read.delim("http://ncslaap.lib.ncsu.edu/tools/norm/downloads/CentralOhioAndTyrone.txt")

## apply the function
samp_norm <- ddply(samp, .(speaker), AnaeNormalize)

## Examine normalization efficacy
## Step 1: Produce means
samp_means <- ddply(samp_norm, .(speaker, vowel.frame), summarize, MF1 = mean(F1), MF2 = mean(F2), MF1_norm = mean(F1_norm), MF2_norm = mean(F2_norm))

## Step 2: Plot them
unnorm <- qplot(-MF2, -MF1, data = samp_means, geom = "text", label = vowel.frame, size = I(2), main = "Unnormalized")+ facet_wrap(~speaker)

norm <- qplot(-MF2_norm, -MF1_norm, data = samp_means, geom = "text", label = vowel.frame, size = I(2), main = "Normalized")+ facet_wrap(~speaker)

print(unnorm)
print(norm)

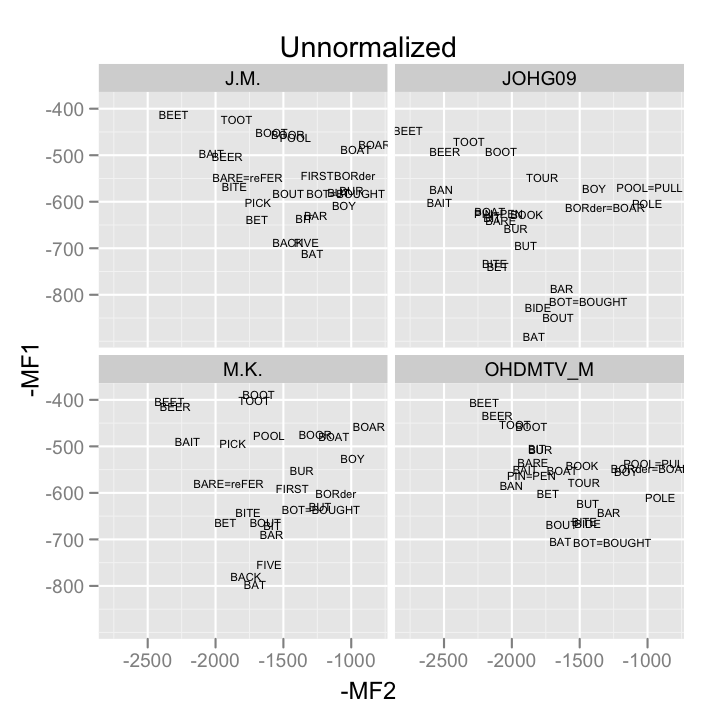
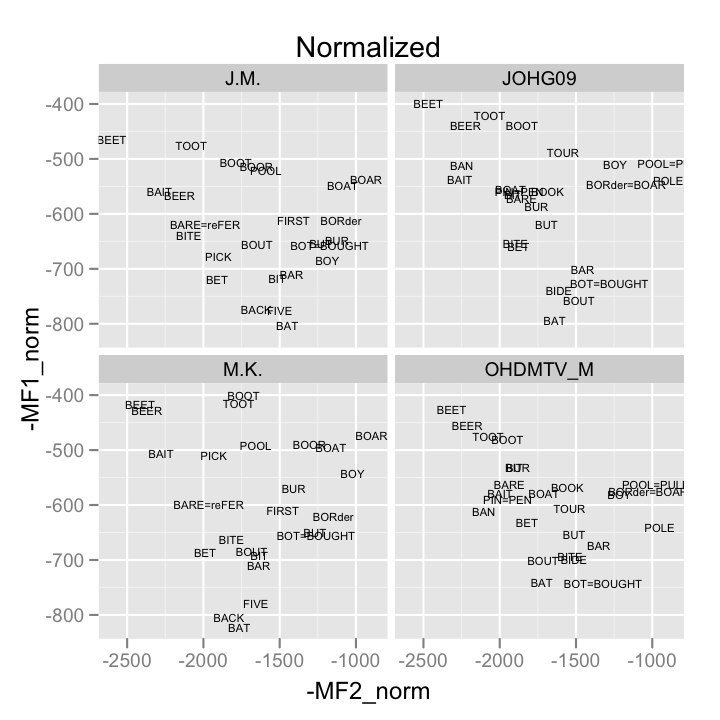
Models example

As a demonstration of the various things you can do with plyr functions, I'll fit a logistic regression for every speaker in my buckeye td deletion data, predicting td deletion by word frequency.

First, I need to define a function.

fitBuckModels <- function(df){
  mod <- glm(DepVar ~ Freq.z, data = df, family = binomial)
  return(mod)
}

Next, load the buckeye data.

buck <- read.csv("http://www.ling.upenn.edu/~joseff/rstudy/data/sbuck.csv")

## zscore the frequency
buck$Freq.z <- (buck$Log_Freq - mean(buck$Log_Freq)) / sd(buck$Log_Freq)

I'll store every model fit in a list, so I'll need to use dlply().

buck_models <- dlply(buck, .(Speaker), fitBuckModels, .progress = "text")

buck_models[1]

Now, I'll access each of those models, and extract their coefficients.

buck_coefs <- ldply(buck_models, coef)

Hadley Wickham's Suggestions

Hadley Wickham (author of he plyr package) suggests the following workflow in the plyr documentation.

Extract a subset of the data for which it is easy to solve the problem.
Solve the problem by hand, checking results as you go.
Write a function that encapsulates the solution.
Use the appropriate plyr function to split up the original data, apply the function to each piece and join the pieces back together.