Summer 2010 — R: Functions

Intro
reshape Package
US War Casualties
Gender Gap
Peterson and Barney

Intro

Effectively deploying plyr functions, and soon enough producing graphics in ggplot2, relies pretty heavilly upon having data in a particular format. However, perhaps it's not always possible to appropriately format data as you collect it, and frequently we inherit data from other sources and researchers who had different concerns when putting together their data. Here, we'll discuss how the reshape package can help us reformat data into other forms.

My approach to this topic will be mostly examples based.

reshape Package

The webpage for the reshape package is located here: http://had.co.nz/reshape/. The suggested documentation on that page is pretty good.

US War Casualties

The first set of data we'll look at comes was linked to by a post on the Guardian Data Blog. The post is about British casualties in Afghanistan, but we'll be looking at data on US war casualties. That data is located here: http://spreadsheets.google.com/ccc?key=phNtm3LmDZEP-WVJJxqgYfA#gid=0

Now, this data is going to require some processing before it's in a workable format, and a lot of that will probably be easier in the text editor of your choice. Download the data from Google Docs as a txt file, then follow these steps in a text editor.

Delete the first line
Delete final 6 lines, starting with "ROUNDING ADJUSTMENTS
Search and replace all commas with nothing
Search and replace all quotes with nothing
Search and replace all hyphens wth nothing
Search and replace all parentheses with nothing
Search and replace all spaces with periods

We still need to code which country the data is coming from into the column names. In principle, it might be a good idea to do this by hand in the raw data. However, we can also do it in a more automated way in R. Save the above changes, then load the data into R using read.delim(). Be sure to set check.names = F in read.delim(). We have a number of columns which have the same names. Ordinarily, this would be bad, and by default R would fix it for us, but for our present purposes we want to leave them as-is.

# Append "Afghanistan_" to the Afghanistan data
colnames(casualties)[2:5] <- paste("Afghanistan", colnames(casualties)[2:5], sep = "_")

#Append "Iraq_" to the Iraq data
colnames(casualties)[6:9] <- paste("Iraq", colnames(casualties)[6:9], sep = "_")

The next step is to "melt" the data with the reshape::melt() function. The arguments that melt() takes are:

data: The data frame containing the data.
id.vars: The columns which define the id variables
measure.vars: The columns which define measure variables. By default, it assumes all non-id variables are measure variables
variable_name: What you want to call the new variable column. The default is "variable", which is pretty fine.

For this casualties data, the only id variable defined in a column is STATE. The other id variable is which country the data came from, which is unfortunately spread out along the columns.

# melt the data
# 1 indicates the column index
casualties.m <- melt(casualties, id = 1, na.rm = T)

# this is an equivalent call to melt()
casualties.m <- melt(casualties, id = "STATE", na.rm = T)

The resulting casualties.m data frame should look something like this:

             STATE                 variable value
  1        ALABAMA Afghanistan_HOSTILE.DEAD     8
  2         ALASKA Afghanistan_HOSTILE.DEAD     1
  3 AMERICAN.SAMOA Afghanistan_HOSTILE.DEAD     1
  4        ARIZONA Afghanistan_HOSTILE.DEAD    19
  5       ARKANSAS Afghanistan_HOSTILE.DEAD     5
  6     CALIFORNIA Afghanistan_HOSTILE.DEAD    75

The column variable contains the measure column names from casualties, and value contains the value from the cell corresponding the rows defined by the id variables, and the column defined by variable.

We haven't got this data in a very usable format yet. We need to separate the country information from the casualty type information. We'll do this by using reshape::colsplit(). Using colsplit() alone will split a given vector along a specific character, and will return a data frame with however many columns this splitting creates. We'll add these new columns back onto the original data frame with base::cbind().

## Let's just see what colsplit() produces
head(colsplit(casualties.m$variable, split = "_", names = c("Country","Type")))

## Add these results back onto the dataframe
casualties.m <- cbind(casualties.m, colsplit(casualties.m$variable, split = "_", names = c("Country","Type")))

Now that we have the data in this format, we can recast the data into almost any shape, including various aggregations. The function to recast data is called reshape::cast(). It takes the following arguments:

data: The data frame containing molten data.
formula: The casting formula. Variables to the left of the ~ define rows, and variables to the right define columns. A pipe (|) following the formula defines subsets.
value: The column to treat as the value. By default, it assumes that a column named "value" is the value column
fun.aggregate: aggregation function
margins: Which margins to calculate grand summaries for

So, if we want to just see how many states we have observations for for each country and casualty type, we can use the following code:

cast(casualties.m, Type ~ Country)

  Aggregation requires fun.aggregate: length used as default
                      Type Afghanistan Iraq
  1           HOSTILE.DEAD          53   56
  2 HOSTILE.WOUNDED.ACTUAL          56   56
  3    HOSTILE.WOUNDED.EST          52   55
  4        NONHOSTILE.DEAD          50   55

As cast() warns us, we didn't define an aggregation function, so it uses length(), or the number of observations for each combination of casualty type and country. It looks as if we have data from 56 states (the 50 states proper, plus 5 territories and Washington D.C.). However, many states don't have reported data for some casualty types for one or more of the countries.

We can also use cast() to calculate total casualties, and median casualties using different aggregation functions. I'll also add column grand summaries.

## Total casualties
cast(casualties.m, Type ~ Country, fun = sum, margins = "grand_col")

                      Type Afghanistan  Iraq (all)
  1           HOSTILE.DEAD         731  3461  4192
  2 HOSTILE.WOUNDED.ACTUAL        4263 27817 32080
  3    HOSTILE.WOUNDED.EST         924  3853  4777
  4        NONHOSTILE.DEAD         272   899  1171

## Median Casualties by State
cast(casualties.m, Type ~ Country, fun = median, margins = "grand_col")

                      Type Afghanistan Iraq
  1           HOSTILE.DEAD         9.0   47
  2 HOSTILE.WOUNDED.ACTUAL        48.5  379
  3    HOSTILE.WOUNDED.EST        12.5   53
  4        NONHOSTILE.DEAD         4.0   10

Overall, the Iraq war has been deadlier. We can also compare this at a state by state level.

## Create a data frame for comparison
## If the combination of ID and measure variables
## produces cells which all only have 1 observation,
## cast will fill the cells with that value
casualties.comp <- cast(casualties.m, STATE + Type ~ Country)

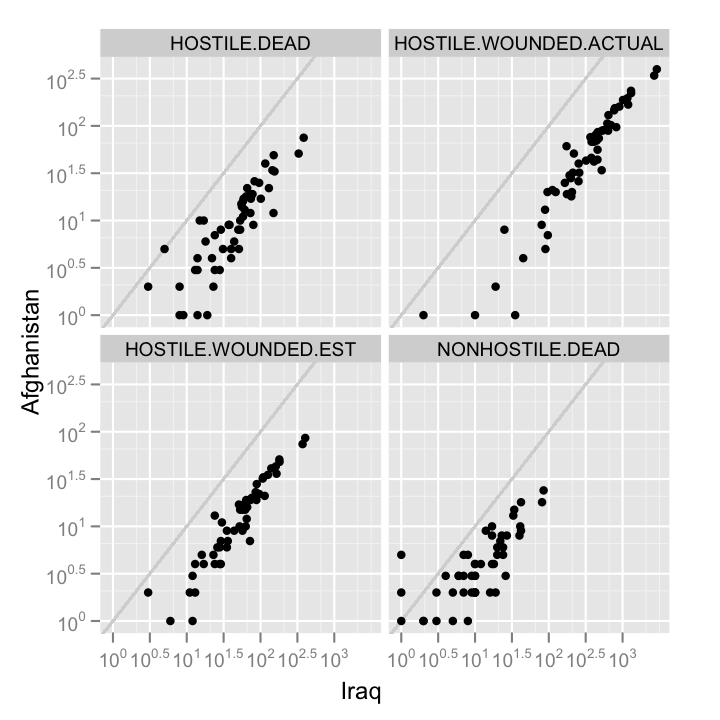
You might also want to compare how one kind of casualty is related to another.

casualties.comp2 <- cast(casualties.m, STATE + Country ~ Type)

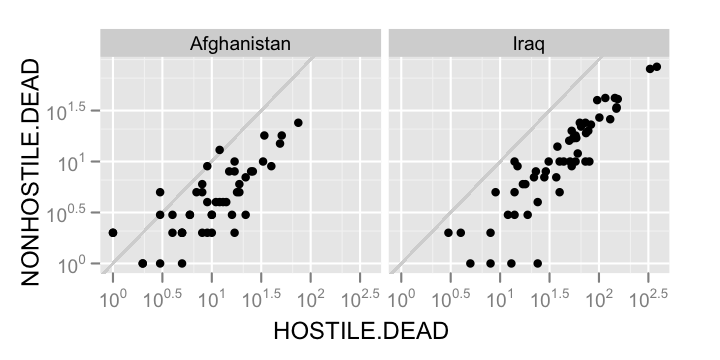
As a final exercise, we might try using the pipe syntax in cast(). This will produce a list of data frames, where every element in the list is defined by the variables following the pipe.

## Using the pipe syntax
casualties.list <- cast(casualties.m, STATE ~ Country | Type)

## Just print all of casualties.list, or
## plot some if it
qplot(Iraq, Afghanistan, data = casualties.list$HOSTILE.DEAD)

qplot(Iraq, Afghanistan, data = casualties.list$NONHOSTILE.DEAD)

It might also help, conceptually, if we recreated the format that the Gaurdian published the data in.

cast(casualties.m, STATE ~ Country + Type)

It might be useful for you to think about the way you structure your data in terms of a cast() formula, per our general discussion of data structure.

Gender Gap

This next data set also comes from a post to the Guardian Data blog about gender inequality. You can find the data here: http://spreadsheets0.google.com/ccc?key=phNtm3LmDZENDfX6fD5PSMw#gid=0

Again, we'll do some pre-processing in a text editor. Download the data from Google spreadsheets, then perform the following steps

Delete the first 8 lines, so that the first line starts "Afghanistan"
Delete the final 3 lines, so that the last line starts "Zimbabwe"
Search and replace all commas with nothing
Search and replace all quotes with nothing
Search and replace all spaces with periods
Search and replace all double tabs with single tabs

Like before, we'll add in the column names in R. I did this part by hand, but it's easier for us all to recreate the same steps if we just copy my code below. Read in the data with read.delim(), being sure to set header = F and na.strings = "..". The next block of code will rename the columns appropriately.

colnames(gender) <- c("Country", "LifeExp_Female", "LifeExp_Male", "Literacy_Female", "Literacy_Male", "Edu_Female", "Edu_Male", "Income_Female", "Income_Male", "Parliament", "Legislators", "Professional", "IncomeRatio")

Looking at the data, there are really two kinds of data sets here. The first compares the status of men and women on a number of different metrics, and the other looks strictly at metrics about women's placement in societies. For our purpose, we'll focus on the former. So, the following code takes the correct subset.

## Only keep the relevant columns
gender1 <- gender[, c(1,2:9)]

Now, like before, we want to melt the data, then use colsplit() to split appart the measurement data from the gender data.

## Melt the data!
gender.m <- melt(gender1, id = 1, na.rm = T)

## Split the variable column!
gender.m <- cbind(gender.m, colsplit(gender.m$variable, split = "_", names = c("Measure","Gender")))

Now we can do some serious stuff. Let's start by checking how balanced the observations are.

cast(gender.m, Measure ~ Gender)

  Aggregation requires fun.aggregate: length used as default
     Measure Female Male
  1      Edu    178  178
  2   Income    174  174
  3  LifeExp    194  194
  4 Literacy    171  171

All contries in the sample have life expectancy data, but no other metric has data from all other countries

Now let's look at median values for each measure.

cast(gender.m, Measure ~ Gender, fun = median)

     Measure  Female    Male
  1      Edu   74.25   72.05
  2   Income 3994.00 7984.50
  3  LifeExp   74.05   68.30
  4 Literacy   89.20   93.70

Women have higher median educational involvement rates and life expectancy, but lower median literacy rates, and much lower median incomes. Let's compare men and women on each metric.

## Create the comparison dataframe
gender.comp <- cast(gender.m, Country + Measure ~ Gender)

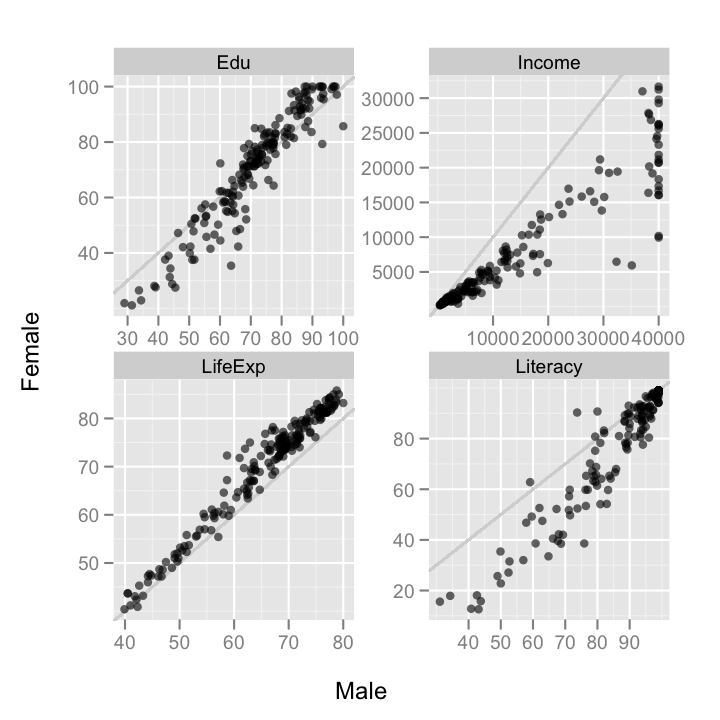
There are a few interesting patterns here. To begin with, it looks mostly like the differences between countries is larger than differences within countries. So, countries with high education, for instance, have both high male and female education. There's also apparently an artificial clipping of reported male incomes. No country reports a mean male income greater than $40,000. I'll be excluding these and other artificially clipped data points in the following plots.

The gender differences within countries are also interesting. The most striking, to my eyes, is that in high education rate countries, women have a higher education rate than men, but in lower education rate countries, men have a higher rate than women.

We should probably also look at how different measures are correlated with eachother.

gender.comp2 <- cast(gender.m, Country + Gender ~ Measure)

Let's start with income and life expectancy.

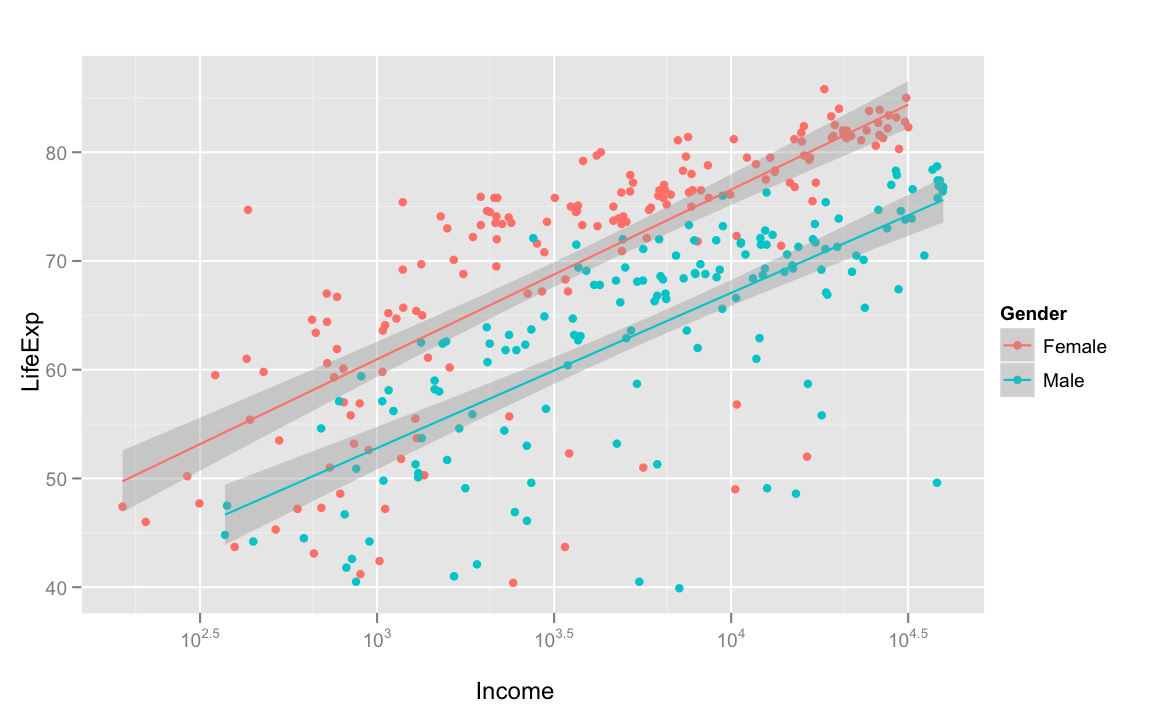
Unsurprisingly, the greater average income, the greater life expectancy is. Women almost always have a higher life expectancy than men of the same average income, but as income increases, life expectancy seems to increase at the same rate for men and women.

Next, education and literacy!

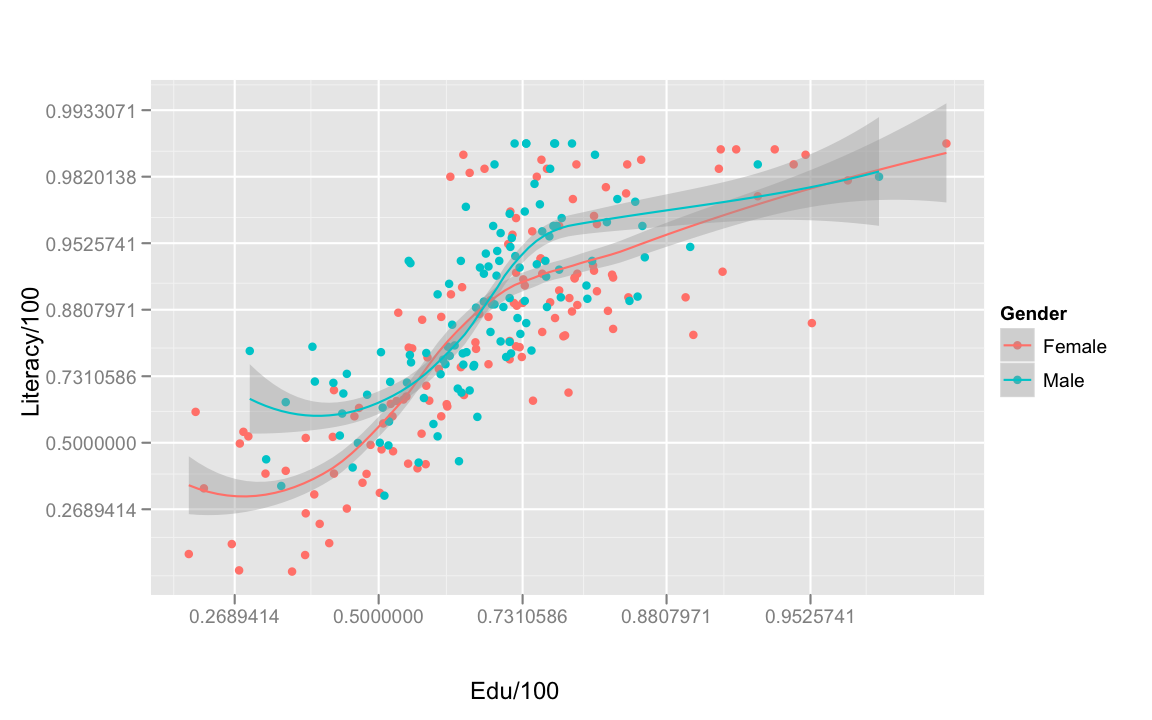
Unsurprisingly, as education increases, so does literacy. The effect of education on literacy also appears to be the same for both genders.

Next, let's look at the effect of education on income!

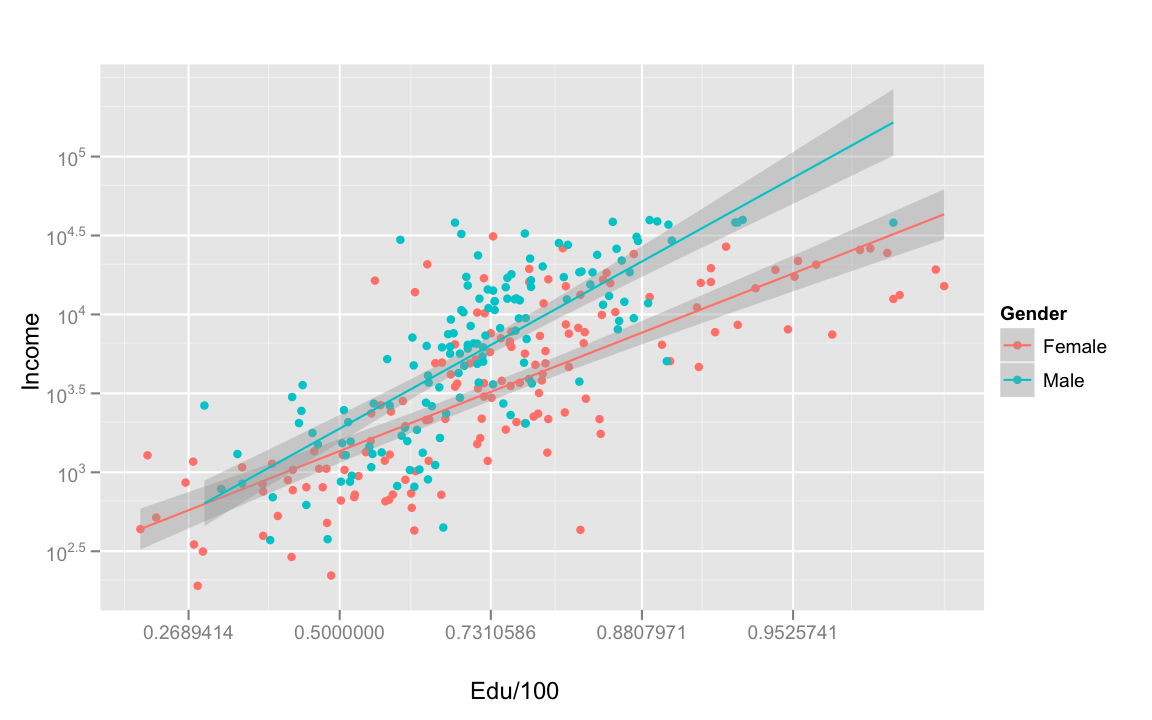
Now that is a strong interaction. Over all, as education increases, average income increases. However, the effect is stronger for men than for women. That is, men get more income bang for their education buck, internationally. For women, the effect of education on income is weaker at the higher education and income end of the spectrum.

We can also visualize this effect by connecting the male and female data points within each country.

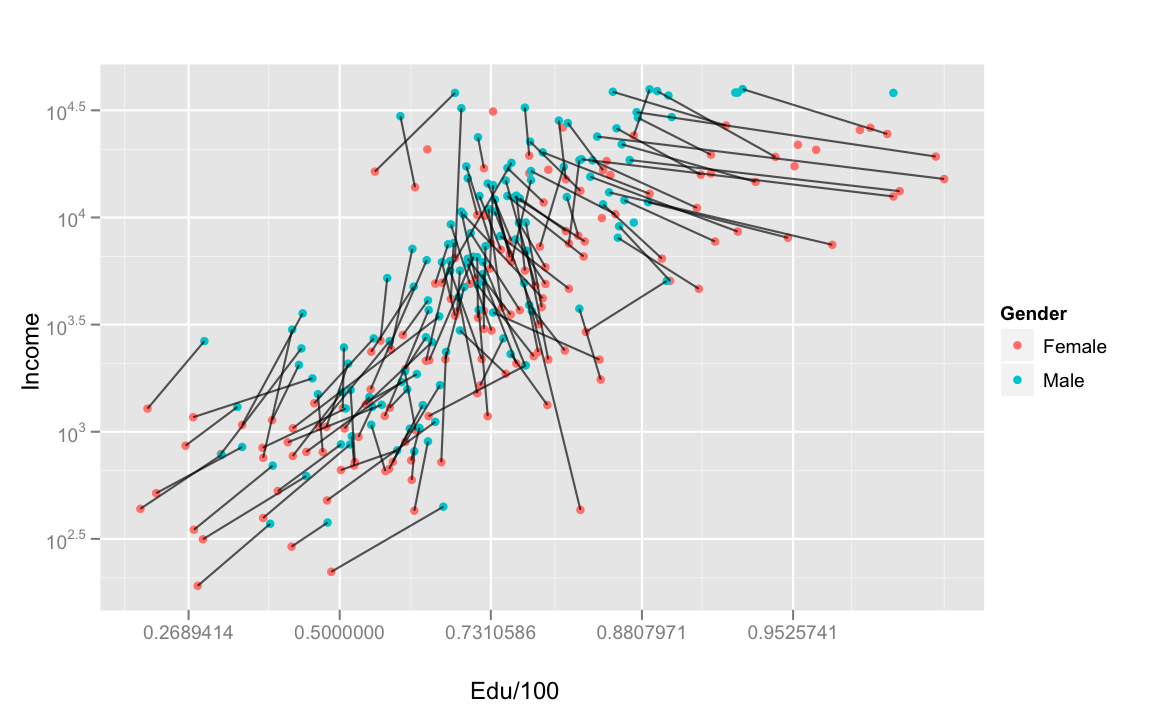
Now, the cross-over pattern in education above makes more sense. The high income countries are also the high education countries, but it's in those countries that women need to have proportionally more education to get the same income benefits. The arbitrariness of this effect should be clear. Women don't appear to be worse learners, as evidenced by there not being a large gender effect on the direct outcome of education, literacy.

Of course, I'm also commiting the environmental fallacy, and maybe others.

Peterson and Barney

I'll use this final set of data to demonstrate some useful aggregation utility in cast(). This data set is acoustic measurements of recordings of 8 repitions of 10 vowels by 76 speakers as collected by Peterson and Barney (1952). It can be found here: http://ling.upenn.edu/courses/cogs501/pb.Table1

First, let's load it into R and clean it up a bit.

## Read in the data
pb <- read.delim("http://ling.upenn.edu/courses/cogs501/pb.Table1", header = F)

## Give meaningful column names
colnames(pb) <- c("Age","Sex","Speaker","Vowel","V1","F0.hz","F1.hz","F2.hz","F3.hz")

## Fix up the age data
levels(pb$Age) <- c("Child","Adult","Adult")
pb$Age <- relevel(pb$Age, "Adult")

Next, melt the data.

pb.m <- melt(pb, id = 1:5)

Now, examine the balance of the data.

## How many measurements by age and sex?
cast(pb.m, Vowel ~ Age+Sex)

Aggregation requires fun.aggregate: length used as default Vowel Adult_f Adult_m Child_f Child_m 1 aa 224 264 64 56 2 ae 224 264 64 56 3 ah 224 264 64 56 4 ao 224 264 64 56 5 eh 224 264 64 56 6 er 224 264 64 56 7 ih 224 264 64 56 8 iy 224 264 64 56 9 uh 224 264 64 56 10 uw 224 264 64 56

## How many speakers by age and sex?
cast(pb.m, Age+Sex ~ ., value = "Speaker",
fun = function(x) length(unique(x)))

Age Sex (all) 1 Adult f 28 2 Adult m 33 3 Child f 8 4 Child m 7

## How many measurements of each vowel by speaker?
cast(pb.m, Vowel ~ Speaker)

So, the data isn't necesarilly balanced in terms of numbers of speakers in each category, but every speaker produced the same number of each vowel.

Now, let's calculate the mean formant values for each vowel in each category of speaker.

pb.means1 <- cast(pb.m, Vowel + Sex + Age + variable ~ ., fun = mean)

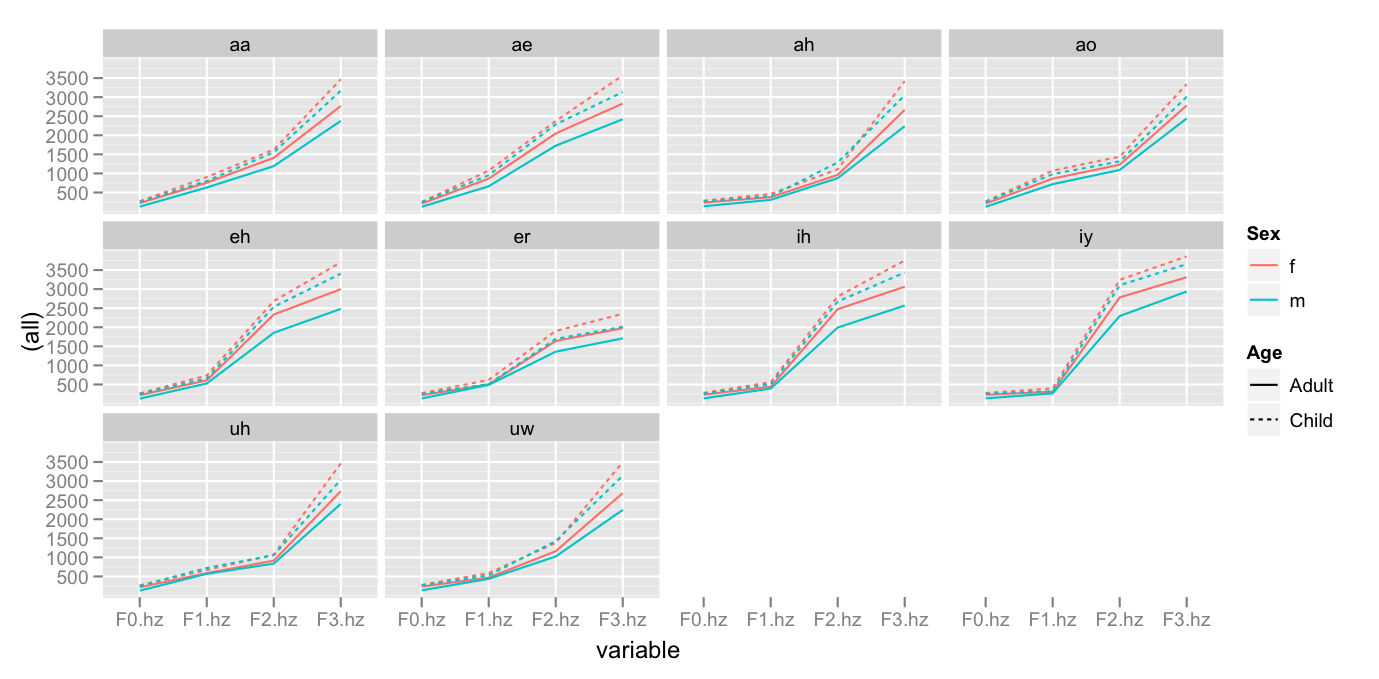
The patterns which seem most clear to me are

The logarithmic distribution of formant values
The order of low to high values go
Adult Male < Adult Female < Child Male < Child Female

To calculate speaker category means:

cast(pb.m, Vowel + Sex + Age ~ variable, fun = mean)

To calculate speaker means: