Summer 2010 — General: Graphics
| <- R: Reshaping | Home |
Contents
Intro
The field of information design is already huge, and growing.
Background Reading
When it comes to reading about information design, it all starts with Edward Tufte's The Visual Display of Quantitative Information. I have found that insights from this and other Tufte works have greatly influenced my own approaches to data visualization, specifically in terms of maintaining graphical integrity, and minimizing use of non-data "ink".
Another classic book in the area is John Tukey's Exploratory Data Analysis. I haven't read this, but I've heard it's very good.
I also suggest subscribing to a few blogs on data visualization. I find that nothing inspires me to try new and better visualizations like seeing new excellent examples. The two blogs I'd suggest most highly are Eager Eyes and Junk Charts. Eager Eyes is maintained by Robert Kosara, who is an academic focusing on information visualization. Apparently they have conferences and everything. Junk Charts is maintained by Kaiser Fung, who is a professional statistician.
A few other blogs which are pretty good, if not more broadly construed (that is, I don't always think they showcase useful or excellent graphics) are Flowing Data, and Chart Porn.
When it eventually comes time to produce graphics with
Why plot?
It's important to think of graphics you produce as a report of your data. Avoid thinking of a plot as a sketch, drawing, illustration, cartoon, decoration, or interpretive art piece of your data. They are merely a spacially and temporally more effective means of reporting your raw data than printing all of the raw data in its entirety.
As was brought up in the study group, it's impossible to simply "report" data in any format without first interpreting it. In fact, the raw data you collect in the first place is interpretive. However, insofar as there is a particular or conventional way you would publish numbers in a large table, and insofar as there are natural properties of those numbers, you want your graphic to accurately represent those properties.
When thinking about numerical data, it's important to think about properties of numbers. Numbers have order, magnitude, and what I'll call contextual magnitude. When you read numbers printed in a table, you have an immediate sense of order and magnitude of the numbers in comparison, and your experience with whatever the numbers represent tells you the contextual magnitude. For example,
| Groups | A | B | Measure | 2 | 5 |
You immediately know that the order is 2 < 5, or A < B, and the magnitude is 5 = 2.5 * 2, or B = 2.5 * A. The contextual magnitude depends on what is being measured. If A and B are bars, and the measure is the cost in dollars of a beer, then we know that B is pretty reasonably priced, and A is super cheap (and probably a dive). If A and B are people, and the measure is their number of legs, then A is what you'd expect, and B has an unbelievably large number of legs.
A graphic is only useful if it accurately conveys at least the order and magnitude of numbers, and ideally it would also convey the contextual magnitude as well. Here is an accurate, and an inaccurate plot of the data above:


The accurate plot has a baseline of 0, the short line goes to 2, and the long line goes to 5. The magnitude of the difference in line height is 2.5x, the same as the data. In the inaccurate plot, the short line still goes to 2, and the long line goes to 5, but the baseline starts at 1.75. The magnitude of the difference between line heights is now (5 - 1.75) / (2 - 1.75) = 13x.
Some people would say, and I agree with them, that the inaccurate plot has misreported the data. I actually think that this is a problem as large as misreported statistical results, or misprinting numbers in a table. Edward Tufte formulates a Lie Factor for graphics, which is given as (Size of the effect in the graphic) / (Size of the effect in the data). For these two graphics, the Lie Factor is 13/2.5 = 5.2.
Here's another example. In this case, I think the problem is an honest editorial mistake, where the graphic designer roughed out the design first, but forgot to update it with the actual data.
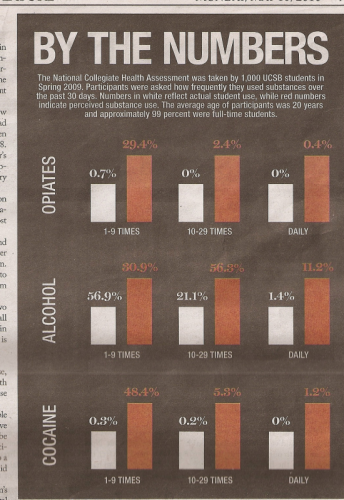
They got the order right, except for one set of bars. We all might think that this is a ridiculous example, but it's a lot easier to fall into a similar trap than you may think. This graphical designer clearly had a rough notion about the size of the effect they wanted to illustrate, and we all have a desire to showcase respectable effects in our research. If the designer so wished, once faced with the actual data, they could have monkeyed with the y-axes of each small multiple, and produced the same exact plot (with the exception of the one order difference). We also have that capacity when generating plots of our own data. My assertion is that the plot here would not be more "honest" or accurate if the axes were labeled, just like it's not more honest or accurate because the data is printed directly on it. If the plot is only accurately interpretable if the data or axes are carefully read, then a reader will understand the plot better if they ignore its graphical elements all together.
Here's the drug data, replotted accurately.

It just so happens that this data is difficult to plot well. Some of the perceived and actual rates of usage are very low, while others are very high. I experimented with plotting this data as perceived to actual ratios instead, but again this produced some huge and some infinite ratios. 48.4 / 0.3 = 161.3 and 2.4 / 0 = ∞
The challenges of creating a plot for this data, and the relatively few numbers involved suggest to me that the data shouldn't be plotted at all, and should just be presented in a table instead, maybe in a fancier version than this:
| Frequency | ||||||
|---|---|---|---|---|---|---|
| Drug | 1-9 | 2-10 | Daily | |||
| Opiates | ||||||
| Alcohol | ||||||
| Cocaine | ||||||
Sometimes, the boldest and best graphical decision is not to make one at all.
Principles
Be parsimonious
A plot which communicates the same data in many ways is not better than a plot which uses fewer ways, or one way. To borrow an example from Tufte, this plot is not particularly offensive:

It accurately represents the data. However, it is overly redundant. The size of the measure is indicated in 7 different ways.
- The height of the left line.
- The height of the right line.
- The height of the top line.
- The height of the filled color.
- The height of the number.
- The value of the number.
- The axis labeling.
Groups in the data are indicated twice.
- The position of the bars on the x-axis.
- The filled colors of the bars.
A better approach would be to eliminate needless redundancy.

Use the appropriate graphical element for the data
There are certain conventions in data graphics, and readers will assume that there are certain properties of your data given these properties' conventional representation. Be sure that your graphical elements communicate correctly. For instance, lines indicate changes within some category across a variable with a meaningful order. So, this plot incorrectly uses a line:

Unless the values along the x-axis have a meaningful order, you shouldn't use lines to connect data at all, and think twice about it if they don't have meaningful magnitudes.
Another, slightly different use of a line is to connect few, but meaningful groups of data points which are plotted in some other
dimensions, like I did in the last plot of
this
You'll also see silly plots like this a lot, especially in newspapers (re: the drugs example above), where the incorrect number of dimensons are utilized. This data plots median income of men and women from Philadelphia and its three immediately neighboring counties in Pennsylvania, broken down by educational attainment.

To read this plot, you need to compare every grouped blue and salmon bar, see that the blue bar is larger than the salmon bar, and make some sort of judgment about how much larger it is given the county and educational level. What's silly is that there are two main dimensions of comparison for each point (Female income and Male income), and we happen to have a simple graphical convention for representing that.

Some people didn't find this graphic immediately intuitive. I think the reason for this is because both axes are measures of the same thing, but across different groups. Usually a two dimensional graphic represents two different kinds of measurements. I think, however, that this plot is a great way to compare different groups which vary in one dimension across many categories, but more familiarity is necessary with this kind of plot before they can be quickly read.
Another way to plot the data is to take the ratio of women's income to men's income, then plot that along education.

This plot represents the same data that women make less than men, but the ratio is better in Philadelphia County. However, it loses the information that this is largely because men's income is greater in the suburban counties. My conclusion is the Male Income by Female Income is the best way to plot the most information.
Finally, don't make pie charts. There are few instances when pie charts are appropriate, and many more where they are very inappropriate. This section of the pie charts wikipedia article sums up the issues nicely. 3D pie charts are never appropriate, and are an enemy of truth and clarity. This blog post sums up those issues.
Check for self sufficiency
Self sufficiency of a graphic is a notion I've read most about on Junk Charts. Like I mentioned above, if the graphic isn't acurately interpretable unless all the data is printed on it, it's not self sufficient, and a table would be a more spacially economic.
Use appropriate and consistent scales and scaling
Sometimes, your data may not be linearly distributed. The most frequent non-linear distribution I see is logarithmic. Things like
population sizes, incomes (see the above plot), durations etc., which all have a fairly hard lower bound, tend to be logarithmic.
The best way to plot this data is either to plot the
Consistency of scales is also very important. Readers will probably immedately interpret all plots as having the same scaling, and if your scaling varies, either in the range of the axes or the aspect ratio of the plot, comparing plots of similar data will become very difficult.


Finally, sometimes the way you scale your plot elements will affect their accuracy. An amateur, but not infrequent error to make in a bubble plot is to scale the radius of a circle to the magnitude of the data. However, people don't see a radius when they look at a circle, they see an area. You should scale the area by the magnitude of the data, or the radius to the square of the data.
Here, I've calculated the face areas of U.S. coins. One sensible way to plot this data is as a set of circles. But, the first plot is wildly inaccurate when the radius is scaled to the face area.

Is the difference between a dime and a quarter really that extreme? A square root y scale does the trick.

Or, we could do the really right thing, and scale the radius to the radius.
