Properties of the DFT and FFT

Calculating the DFT

The equations for the DFT (Discrete Fourier Transform) and inverse DFT, using Matlab-style indices, are given below:

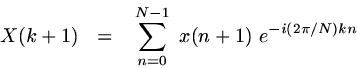
$\begin{displaymath} X(k+1)~~ =~~ \sum_{n=0}^{N-1}~x(n+1)~e^{-i(2\pi/N)kn} \end{displaymath}$	Discrete Fourier Transform (Matlab-style indices)
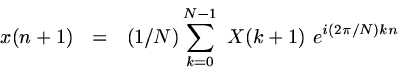
$\begin{displaymath} x(n+1)~~ =~~ (1/N) \sum_{k=0}^{N-1}~X(k+1)~e^{i(2\pi/N)kn} \end{displaymath}$	Inverse Discrete Fourier Transform (Matlab-style indices)

The DFT is useful both because complex exponentials are eigenfunctions of LSI systems -- as previously explained -- and also because there are very efficient ways to calculate it. For an N-length vector, a direct implementation of the formula above would require N complex multiply-adds for each of N frequency-domain coefficients, or a totals of N^2 complex multiply-adds, plus logic. The FFT (Fast Fourier Transform) is not a separate transform, but just a way to calculate the DFT that factors the equations in a way that can reduces the total amount of calculation by a considerable degree. The exact reduction depends on the factorization of the length of the vector to be transformed, and the exact version of the algorithm used. For a vector length that is a power of 2 (e.g. 128 or 1024 or 4096), the cost is not N^2, but rather N*log2(N)/2. For example: 4096^2 = 16,777,216; 4096*log2(4096)/2 = 24,576.

We're not going to spend much time on FFT algorithms in this course -- it doesn't change the nature of the DFT or the principles of its use, although of course it does make it much more practical to calculate the DFT of long vectors. If you're interested in the clever recursive factorization involved, check out the Wikipedia page, or this more explicit explanation.

The fft functions in Matlab and Octave automatically implement an appropriate factorization of the DFT, if one is available.

DFT/FFT for real inputs

There is another way to achieve a (more modest) speed-up in DFT/FFT calculations. As defined, the DFT operates on a vector of N complex numbers to produce another vector of N complex numbers. We normally apply the DFT to vectors of real numbers, with the result that half the values in the DFT output are complex conjugates of the other half of the values.

There is a fairly simple way to take advantage of this redundancy to calculate the DFT of a real vector as if it were a vector of half the length. The explanation is given below, in two stages. I believe that Matlab automatically applies this method to real-valued input vectors.

1. Calculating two real-valued DFT's as one complex-valued DFT. Suppose we have two real-valued vectors a and b. We can create a complex vector c = a + i*b. Since the DFT is a linear transformation, DFT(c) = DFT(a) + i*DFT(b). The trick is to figure out how the sum is done -- and how to undo it to separate the transforms of a and b -- since both DFT(c) and DFT(b) are complex vectors.

2. Splitting a DFT into two of half the size. This is just one step of the factorization into even-numbered and odd-numbered subsequences, as detailed here.

Properties of the DFT

Linearity

The transform of a sum is the sum of the transforms: DFT(x+y) = DFT(x) + DFT(y). Likewise, a scalar product can be taken outside the transform: DFT(c*x) = c*DFT(x). These follow directly from the fact that the DFT can be represented as a matrix multiplication.

Circular shift of input

If f is circularly shifted by m (i.e. the elements of f are moved m places to the left, with elements that "fall off" one end of the sequence appearing at the other end), then the magnitude of the DFT of f is unchanged, while the phase of the DFT of f is shifted by an amount that depends linearly on the index of the DFT element.

DFT of an impulse:

>> f=[1 0 0 0 0 0 0 0]; 
>> fftshift(abs(fft(f)))
ans =
     1     1     1     1     1     1     1     1
>> fftshift(angle(fft(f)))
ans =
     0     0     0     0     0     0     0     0
>> norm(f)
ans =
     1         %% geometric length of f is 1
>> norm(fft(f))
ans =
    2.8284     %% geometric length of fft(f) is sqrt(8)
>> norm(abs(fft(f)))
ans =
    2.8284     %% geometric length of

DFT of a sinusoid

>> x = (0:7)*2*pi/8;
>> fftshift(abs(fft(cos(3*x))))
ans =
  Columns 1 through 7 
    0.0000    4.0000    0.0000    0.0000    0.0000    0.0000    0.0000    4.0000

Note non-zero values at frequencies -3 and 3.

>> fftshift(angle(fft(cos(3*x))))
ans =
         0    0.0000   -1.8630    0.1244    3.1416   -0.1244    1.8630   -0.0000

Note zero phase at frequencies -3 and 3, corresponding to cosine function input. What would phase be with sin(3*x) as input? Also, remember that phases of components not really there (i.e. all the others) are numerical artefacts.

Duality of circular convolution and element-wise multiplication

For two length-N sequences x and y, the circular convolution of x and y can be written as

where index values outside the range of 0 to N-1 are interpreted "circularly", that is as referring to a periodically-repeated version of x or y. Thus x[-1] is the same as x[N-1].

This is just like regular convolution of the same input sequences, except that it returns a vector of the same length as the two inputs, and it assumes periodicity to get values "off the edge", rather than assuming zero values.

If we write circular convolution of x and y as x#y, and element-wise multiplication of x and y in Matlab fashion as x.*y, then

DFT(x # y) = DFT(x) .* DFT(y)

and

DFT(x .* y) = DFT(x) # DFT(y)