Problem Set #6

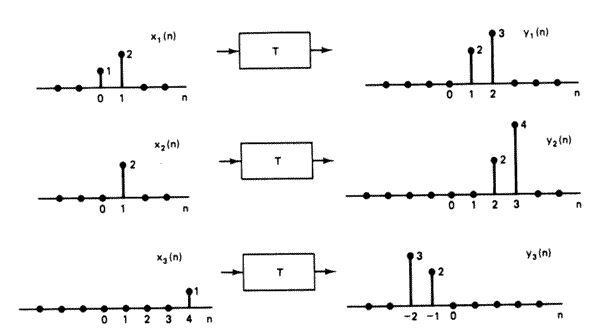
1. (Oppenheim and Shafer 1989 p. 68). The system T in the figure below is known to be time-invariant. When the inputs to the system are x1[n], x2[n] and x3[n], the responses of the system are y1[n], y2[n], y3[n] respectively.
   1. Could the system T be linear? Explain. (Hint: Can you express one of the the inputs as a sum of scaled and shifted copies of other inputs? If so, what does this predict about the outputs?)
   2. If the input x[n] to the system T is delta[n] (i.e. a unit impulse at time 0), what is the system response y[n]?
   3. Determine all possible inputs x[n] for which the response of the system T can be determined from the given information alone.
   
   
   

    

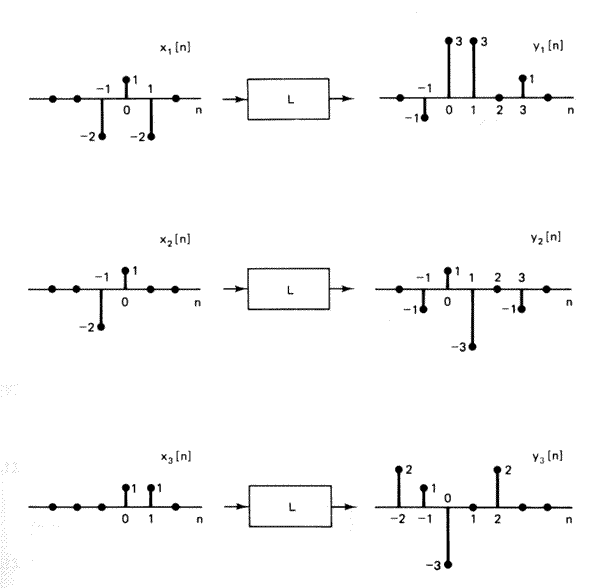
2. (Oppenheim & Shafer 1989 p. 69) The system L in the figure below is known to be linear. When the inputs to the system are x1[n], x2[n], x3[n], the response is y1[n], y2[n], y3[n] respectively.
   1. Could the system L be time-invariant? Explain.
   2. If the input x[n] to the system is delta[n], what is the system response?
   
   
   

    

3. Create a vector of length 24 containing an impulse at location 5, a step edge at location 12, and a unit-slope ramp starting from location 18. For example:
   
   X=zeros(24,1); X(5)=1; X(12:24)=1; X(18:24)=(X(18:24)+(1:7)');
   
   Convolve this signal with the ``two-point averager'': [0.5, 0.5], and the ``two-point differencer'': [0.5,-0.5]. How does the differencer respond to the various features?
4. Show that the two convolution results computed above may be added together to reconstruct the original signal. Would this be true for an arbitrary input signal? Why?
5. Construct a matrix that will represent the action of a shift-invariant linear system (the non-zero elements of) whose impulse response is [1 2 3]', on an arbitrary seven-element input vector. (Hint: the input vector will have the dimensions 7x1; the matrix will thus have to have the dimensions Nx7, where 'N' is chosen so that the result will have the right size for the consequences of convolving a seven-element vector (the input) with a three-element vector (the impulse response).
6. Write a MATLAB function that will imitate the basic behavior of the built-in function conv(a,b), but will accomplish it by constructing a matrix M out of 'b' and then multiplying 'a' by M. How does 'b' appear in the rows and columns of M?
7. Write a Matlab function mksine to construct a vector of samples of a sine function. The function should take arguments size, frequency, amplitude, and phase.
8. Make three sampled sinusoids of size (i.e. number of samples) 256; frequencies 1, 2, and 3; amplitude of 1; and phase of 0. Create a random 32-element impulse-response (using rand()) and convolve your sinusoids with it, using circular convolution as defined in the lecture notes. (You may want to call your function something like mycconv(), since there is Matlab function cconv() with somewhat different properties.)
   
   In each case, the result should be a sinusoid of the same frequency but with different amplitude and phase. What are the new amplitudes and phases?
   
   
9. For the frequency 1 sinusoid, repeat the experiment using the same impulse-response but picking a  random amplitude and phase for the sinusoidal input. What is the relationship between the amplitude and phase of the input and the amplitude and phase of the output? Can you predict what the result would be for a new choice of input amplitude and phase?
10. Repeat the experiment using sinusoids of frequency 2.
11. Try taking the inner product of your random impulse-reponse with sine and cosine waves of various frequencies (especially 1 and 2). You can do this by creating sine and cosine waves with 32 elements; or by padding your impulse response with zeros to length 256. How might you use those inner products to predict the results of the convolution experiments?