Linguistics 520: Lecture Notes 1

9/9/2013

Topics for the first sequence of lectures:

1. What is sound? Be able to define and calculate frequency, period, amplitude, wavelength, power...
2. How does the human vocal tract create and shape sounds?
3. How does human speech encode words?
4. What else is in speech besides words?

Sound is variation in pressure. For our purposes, the transmission medium is air, and we'll be interested in variations that take place on a time scale ranging from about 1/20 of a second to about 1/20,000 of a second. (Higher frequencies are interesting to bats, and much lower frequencies are interesting to meteorologists...)

We'll consider both traveling waves, where the variation in pressure moves through the air as longitudinal or compression waves, and also in standing waves, where reflections create resonances (as in vocal tract formants).

If we measure the pressure variation at a fixed point in time for a sinusoidal sound wave, and plot the measurements as a function of time, we get something like this:

The period T is the time it takes for the same part of the wave's regular repetition to pass by our measurement point again.

Of course, this presupposes that the pressure variation actually has a regular pattern of repetition, i.e. is periodic. Real-world sounds are never perfectly periodic, though they may be pretty close to periodic -- "quasi-periodic" -- if we limit our attention to a small enough span of time. Here's about 0.025 (25 milliseconds) of a speech wave, with one of the quasi-periodic regions marked with an arrow:

We'll learn more later about what else is going on in a signal like this.

Obviously, the period T is measured in units of time, i.e. seconds or fractional seconds. (We could measure the period in hour or days or fortnights or centuries, but seconds are already inconveniently long.) And just as obviously, the frequency -- the number of repetitions per second, is the inverse of the period.

In other words, F = 1/T and T = 1/F.

If the period T is measured in seconds, then the frequency F = 1/T is in units of cycles per second, more commonly called hertz (symbol Hz). This unit is named after the German physicist Heinrich Rudolf Hertz.

Instead of plotting the pressure variation at a point as a function of time, we could measure the pressure variation in space, along the direction of traveling-wave propagation. And the plot will look exactly the same as the time function, except that the horizontal axis is now space rather than time, like this:

Now the span between waveform repetions is an extent of space rather than time: the wavelength. It's conventional to symbolize the wavelength with λ (the Greek letter lambda). How is the wavelength related to the period and the frequency? In other words, how can we express λ in terms of T, or λ in terms of F, or T or F in terms of λ?

This is easy, except that we need to know one more thing. The wavelength for a sound of period T is obviously the distance that the wave travels in time T -- and to determine this distance we need to know how fast the wave is moving, i.e. the speed of sound, which is conventionally symbolized by C. Wikipedia tells us that

In dry air at 20 °C (68 °F), the speed of sound is 343.2 metres per second (1,126 ft/s). This is 1,236 kilometres per hour (768 mph), or about a kilometre in three seconds or a mile in five seconds.

The speed of sound in air is essentially independent of frequency and of air pressure. It changes slightly with temperature (increasing by about 0.6 m/s for each degree celsius), and with humidity (increasing slightly in more humid air). Thus in dry air (0% humidity) at at 0 °C, the speed is about 331 m/s; in dry air at 40 °C the speed is about 355 m/s. At 0 °C, the speed in 100% humidity is only about 0.3 m/s greater than in dry air. At 40 °C, the speed in 100% humidity is about 3 m/s greater than in dry air.

You can calculate exact figures here -- but you won't go far wrong, for purposes of this course, by taking the speed of sound to be 340 m/s.

Obviously the distance traveled in T seconds at 340 m/s is T*340, or keeping track of the units,

λ meters = T seconds * 340 meters/second

So a period of 1/100 of a second would yield a wavelength of λ = 340/100 = 3.4 meters.

More abstractly, the equation to remember is

λ = T*C

or (since F= 1/T)

λ = C/F

You should get comfortable with translating among period, amplitude, and wavelength -- you'll need to do it frequently in any work in instrumental phonetics. And it will be on quizzes and exams in this class! So if it's not obvious to you what the frequency of a sound with period 0.076 seconds is, or what the period of a sound with frequency 796 Hz is, or what the wavelength of a sound with frequency 1835 Hz is, etc., you should practice.

In both time and space, we graphed amplitude on the vertical axis in the plots above. If we're talking about actual sound waves, amplitude is just (variations in) air pressure. Pressure is force per unit area, and can be measured in pascals (newtons per square meter), but we will hardly ever be measuring actual pressures in this course, though we'll need to learn what people mean when they talk about sound pressure level (SPL), and we'll demonstrate how sound pressure levels are measured.

In the case of the recorded sounds we'll be analyzing, pressure variations have been transduced (by a microphone) into voltage variations, and these in turn have been digitized -- measured at regular intervals and thereby turned (like everything else in a computer) into a series of numbers. We'll learn later about sampling frequency (how many times per second the voltage is measured), about how many different levels of quantization are (potentially) used, and so on.

We care a lot about the specific values of sound period, frequency, and wavelength -- but we usually don't pay any attention to the specific values on the amplitude scale. There are good physical and evolutionary reasons for this difference in attitudes.

To understand this point, you need to know a few crucial facts:

1. The speed of sound is the same for all (relevant) frequencies.
2. Because a sound normally propagates in all directions, spreading its energy over the surface of an expanding sphere, and because sound energy (like all energy) is conserved, sound power decreases with distance from the source according to an inverse square law.
3. The propagation of sound in air is linear, which means (among other things) that if we encounter two sounds X and Y simultaneously, the result is just the sum X+Y.

Therefore, when sounds travel through the air from their sources to our ears (or our microphones), the periods and frequencies and wavelengths that make them up are preserved, at least to point where the amplitude gets to be so low that we can't sense them anymore. And those qualities are what we use to analyze the sounds we hear, whether to understand speech or to perform what's called "auditory scene analysis". However, the amplitude will s vary over a wide range in ways that aren't determined by the nature of the sound source. Step away from the source a little, and the amplitude gets smaller -- step toward it, and the amplitude is bigger.

It does matters how relatively intense sounds are -- this helps us to figure out where they're coming from, for example, and we care if the amplitude is too low for us to hear clearly, or so high that it's painful. And relative amplitudes are relevant to stress, emphasis, and other linguistic and paralinguistic features of speech. (And relative amplitudes are even more relevant when we separate sound into different frequency components...) But quantifying the exact level of a sound is not very useful, except to audiologists. Ears and brains don't do it, and phoneticians usually don't either.

There are at least two kinds of amplitude that you'll need to learn about: peak amplitude and root-mean-square amplitude (usually called "RMS").

Here's a plot of a small region (about 6 milliseconds) of a speech waveform:

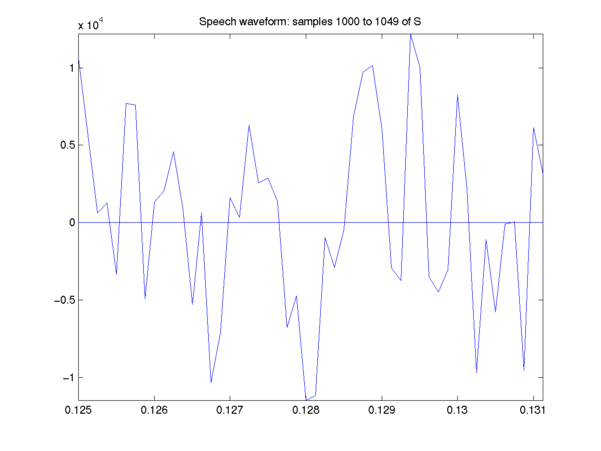
Since this is a piece of a digitized waveform, it's more realistic to plot it this way:

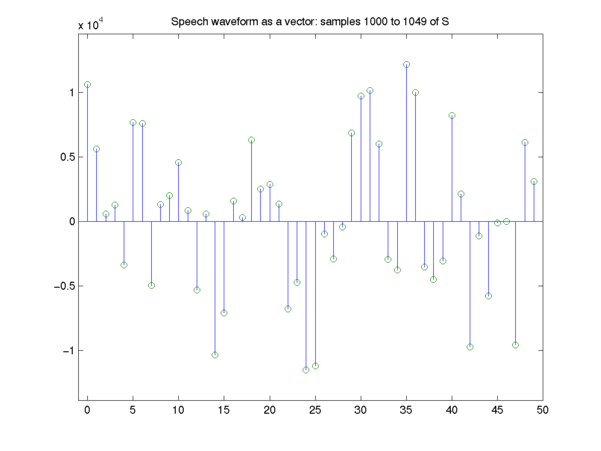
Let's zero in on just the first six samples:

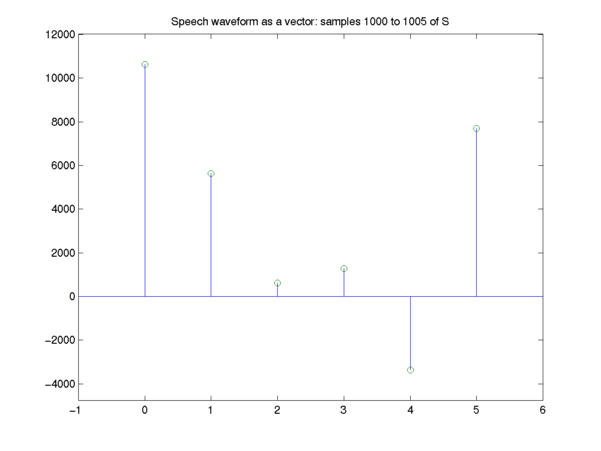
The actual six numbers in this case are:

10622 5624 614 1280 -3363 7694

The peak amplitude is just the maximum value of the signal in the region in question -- here it's 10,622 (in meaningless arbitary units).

But it's more useful and relevant to calculate an amplitude value that's representative of the distribution of values in the signal as a whole, not just the single maximum value. The best way to do this is to square the values, take the average, and then take the square root. In the useful interactive programming language Octave (= the free version of Matlab), we could do it like this:

     >> x = [10622 5624 614 1280 -3363 7694];
     >> x.^2
     ans = 112826884    31629376      376996     1638400    11309769    59197636
     >> mean(x.^2)
     ans =  3.6163e+07
     >> sqrt(mean(x.^2))
     ans =  6013.6

You're not going to have to calculate the squares of sample values, etc., or (for this course) even program a computer to it for you. But you should know what "RMS" means.

And now there's just one last thing for today: power vs. amplitude, and measuring levels in decibels.

Let's get right to the stuff that you need to memorize:

1. Sound intensity is proportional to (RMS) amplitude squared (and sound power is also proportion to RMS squared).

2. Levels are always calculated as logarithms of ratios of sound intensities (or equivalently as ratios of sound powers). Some examples of such levels: "sound pressure level" (SPL); "signal to noise ratio" (SNR); spectral amplitudes; spectral transfer functions of filters; etc. These are comparisons of the strength of one quantityl to the strength of another: SPL is the strength of a sound compared to the strength of some reference sound, usually taken to be the weakest sound that a normal human can hear; SNR is the strength of the "signal" compared to the strength of the "noise" (where "noise", like "weeds", is defined as whatever you don't want in your acoustic garden); spectral amplitudes are the strength of the sound in one frequency regions compared to the strength of the sound in another. In all cases, we compare strengths by taking the log of the ratio of intensities.

3. The unit equal to the base-10 log of a ratio of sound intensities is the bel, named after Alexander Graham Bell (with the spelling changed so as not to make people think of the sound of tinkly bells, I think). Because base-10 logs yield uncomfortably large units, such levels are conventionally denominated in decibels -- one bel is 10 decibels, of course, just as one liter is ten deciliters. The conventional abbreviation for decibel is dB.

4. For sounds x and y, if their intensities are I(x) and I(y), then the ratio of intensities is I(x)/I(y), and the ratio in decibels will be

10*log10(I(x)/I(y))

And since the intensity is the RMS squared, and since

log10(x²) = 2*log10(x)

it follows that the corresponding level in decibels is

20*log10(RMS(x)/RMS(y))

5. And since division of numbers is subtraction of their logs, if (for instance) the sound level of the speech region of a recording is SPEECH dB, while the sound level of the background is BACKGROUND dB, then the signal-to-noise level is roughly (SPEECH-BACKGROUND) dB. This is another reason to use logarithmic units, since "levels" (ratios of intensities) turn into differences, which are easy to estimate accurately in your head.

Praat makes it easy to get sound levels in dB. If you turn on the Intensity>>Show intensity... menu item, Praat will show intensity in dB as a yellow line in the display window (typically on top of the spectrogram). And if you place the cursor on top of that line, Praat will show the (numerical) level in dB in the right-hand margin of the plot.

Note that dB measures quickly translate into very large intensity (and amplitude) ratios. Thus an SNR of 50 dB means that the signal intensity is 10⁵ = 100,000 times larger than the noise intensity. (Since the sound intensities are proportional to the amplitudes squared, the signal amplitude will only be 316.23 times larger than the noise amplitude. But it's still a big difference, e.g. in how the waveforms look on the computer screen.)

Now, at this point you might well be asking, Why do we always calculate levels in terms of intensities rather than amplitudes? And why is intensity proportional to amplitude squared? You don't really need to know the answers to the these questions, as long as you've mastered the points listed above. But if you're curious, there's some discussion here -- some especially useful answers are this one and this one, but the whole discussion is interesting.