 b
b
 b
b c
c
(N.B. These are the online lecture notes for lectures 10 and 11)
We can communicate a lot without words, by the expressive use of eyes, face, hands, posture. We can draw pictures and diagrams, we can imitate sounds and shapes, and we can reason pretty acutely about what somebody probably meant by something they did (or didn't do).
Despite this, we spend a lot of time talking. Much of the reason for this love of palaver is no doubt the advantage of sharing words; using the right word often short-cuts a lot of gesticulating and guessing, and keeps life from being more like the game of charades than it is.
Given words, it's natural enough to want to put them together.
Multiple ``keywords'' in a library catalog listing can tell us more about
the contents of a book than a single keyword could. We can see this effect
by calculating the words whose frequency in a particular book is greatest,
relative to their frequency in lots of books. Here are a few sample computer-calculated
lists of the top-20 locally-frequent words, for each of a range of books
on various topics:
``Earth and other Ethics:'' moral considerateness bison whale governance utilitarianism ethic entity preference utilitarian.
`` When Your Parents Grow Old:'' diabetes elderly appendix geriatric directory hospice arthritis parent dental rehabilitation
``Madhur Jaffrey's Cookbook:'' peel teaspoon tablespoon fry finely salt pepper cumin freshly ginger
For example, the last word list gives us a pretty good clue that we are dealing with a cookbook, and maybe even what kind of cuisine is at issue, but it doesn't tell us how to make any particular dish.
Just adding more words doesn't help: the next ten in order
from the (Indian) cookbook are:
This is the principle of compositionality: language is
intricately structured, and linguistic messages are interpreted, layer
by layer, in a way that depends on their structure.
This line of thinking gives us a first answer to the question
"why bother with syntax?" The answer is "so as to be able to communicate
an infinity of ideas with finite (and simple) means."
Unlike in the arithemetic examples just given, ordinary language doesn't normally have explicit parentheses (although sometimes we modulate pitch and timing to try to indicate the grouping of words). This lack of vocalized parentheses sometimes leads to uncertainty about exactly what the structures are: thus a ``stone traffic barrier'' is probably a kind of traffic barrier, and not a way of dealing with stone traffic, while ``steel bar prices'' are what you pay for steel bars. We know this because we know what interpretations make sense: just the fact that we have three English nouns in a row does not specify either the structure (1 (2 3)) or the structure ((1 2) 3).
The number of logically possible alternative structures, assuming each piece is made up of two elements, grows rapidly with phrase length. For instance, ``Pennsylvania state highway department public relations director'', which contains seven words, has 132 logically possible consituent structures, each of which has many possible meaning relationships between its elements. We understand it fairly easily, all the same, because we are already familiar with phrases like "public relations", "state highway", and so on.
In contrast, consider the phrase ``process control block
base register value,'' taken from the technical manual for a once-popular
minicomputer. To those familiar with the jargon, this clearly means
"the value of the base register for the block of memory dealing with process
control," i.e. a structure like
Ambiguity of constituent structure is not the only problem here. English noun compounds also suffer from semantic vagueness in the relations between the words, even when we know the constituent structure. Thus ``peanut oil'' is oil made from peanuts, but ``hair oil'' is not oil made from hair; a ``snow shoe'' is a shoe to walk on snow with, but a ``horse shoe'' is not a shoe to walk on horses with.
Languages also establish conventions about the interpretation of word order. For instance, although English compound nouns are about as loose a syntactic system as you ever see, English does regularly put the head (or dominant element) of noun compounds on the right, so that ``dung beetle'' is a kind of beetle, while ``beetle dung'' would be a kind of dung.
This is not logically necessary -- other languages, such as Welsh and Breton, make exactly the opposite choice. Thus Breton kaoc'h kezeg is literally the word for ``manure'' followed by the word for ``horse,'' i.e. ``manure horse'' in a word-by-word translation. However, Breton kaoc'h kezeg means ``horse manure,'' that is, manure produced by a horse, and not (say) a horse made of manure, or a horse dedicated to producing manure, or whatever "manure horse" in English might mean.
This situation is common: individual human languages often have quite regular patterns of word order in particular cases, even though these patterns may vary from language to language. Thus English expects determiners (words like ``the'' and ``a'') to come at the beginning of noun phrases, and adjectives to precede nouns they modify, so that we say ``the big cow'' and not (for instance) ``cow big the.''
As it happens, Mawu expects determiners to come at the end of noun phrases, and adjectives to follow the nouns that they modify, and so the equivalent phrase is Mawu is ``nisi wo o,'' which is literally ``cow big the.''
Word order is more rigid in some languages than in others. Putting it another way, in some languages word order is more rigidly dependent on grammatical relations (roughly, the structures that specify who did what to whom), while in other languages, word endings do more work in expressing grammatical relations, and word order can be used for other purposes, like indicating subtle gradations of discourse prominence.
Not always.
Let's suppose that we knew what words mean, and a lot about how to put meanings together, but we had no particular constraints on syntactic structure. In this imaginary condition, we don't care about the order of adjectives and nouns, nor where verbs should go relative to their subjects and objects. There are some general principles that might help us, such as that semantically-related words will tend to be closer together than semantically-unrelated words are, but otherwise, we are back with the ``word stew'' we imagined earlier.
Under these circumstances, we could still probably understand a lot of everyday language, because some ways of putting words together make more sense than others do.
We are in something like this condition when we try to
read a word-for-word gloss of a passage in a language we don't know. Often
such glosses can be understood: thus consider the following ancient Chinese
proverb (tones have been omitted, but distinguish zhi "it" from
zhi "know"):
huo
zhong hu di,
mo zhi zhi bi.
misfortune heavy than earth,
not it know avoid.
Most people can figure this out, at least approximately, despite the elliptical style that does not explicitly indicate the nature of the connections between clauses, and despite the un-English word order. Few of us will have any trouble grasping that it is luck that is (not) being carried, and misfortune that is (not) being avoided, because that is the only connection that makes sense in this case.
A scholar will explain to us, if asked, that this proverb exemplifies a particular fact about ancient (pre-Qin) Chinese, namely that object pronouns (``it' in this case) precede the verb when it is negated. This syntactic fact would have helped us figure out that ``it'' is the object of ``avoid'' rather than the subject of ``know''--but we guessed that anyway, because things made more sense that way.
Sometimes the nature of the ideas expressed doesn't make
clear who did what to whom, and we (or modern Chinese speakers), expecting
objects to follow verbs, might get confused. Thus the phrase
When there is a lesion in the frontal lobe of the left cerebral hemisphere, the result is often a syndrome called Broca's aphasia. The most important symptom is an output problem: people with Broca's aphasia cannot speak fluently, tend to omit grammatical morphemes such as articles and verbal auxiliaries, and sometimes can hardly speak at all. Their comprehension, by comparison, seems relatively intact.
However, under careful study their ability to understand
sentences turns out to be deficient in systematic ways. They always do
well when the nouns and verbs in the sentence go together in a way that
is much more plausible than any alternative: ``It was the mice that the
cat chased,'' ``The postman was bitten by the dog,'' and so forth. If more
than one semantic arrangement is equally plausible, e.g. ``It was the baker
that the butcher insulted,'' or if a syntactically wrong arrangement is
more plausible than the syntactically correct one, e.g. ``The dog was bitten
by the policemen,'' then they do not do so well.
There have been various motivations, the most important being:
The overall enterprise is truth conditional. A language (whether logical or natural) is defined in a way that associates with each expression in the language another expression defining the conditions under which it "holds" or "is the case." This definition is accomplished recursively, just as in our earlier example of the recursive definition of the value of arithmetic expressions. The general approach can be extended to encompass a formal model of the unfolding of information in discourse, so that many aspects of pragmatics as well as semantics can be treated.
The strength of this tradition has been its careful attention to giving an account of meaning, especially in such troublesome areas as quantifiers ("some", "every", "few"), pronouns, and their interactions. It is not easy to provide a recursive truth definition for sentences like "Every farmer who owns a donkey beats it," or "someone even cleaned the BATHROOM," but in fact the semantic properties of such sentences can be predicted by contemporary theories in this area.
Getting such meanings right, in a formal approach, is difficult and complex, and many aspects of natural language semantics have not been investigated, much less solved. Exploring new areas of meaning has therefore been the main focus of research in this tradition.
The details of natural language syntax have generally not been as interesting to the "logical grammarians," though of course they have insisted on providing precise and flexible formalisms for characterizing syntactic structures. A 1958 paper by Joachim Lambek, entitled "The mathematics of sentence structure," provides a lucid example of one approach.
In recent years, some linguists have begun to use such techniques to explore subtle and interesting properties of natural-language syntax, as this web page for a recent short course by Oehrle and Moortgat shows. However, investigators who are interested in natural language syntax in its own right have generally followed another course.
For the most part, this work took place in the tradition of the humanities, rather than that of mathematics or the natural sciences. In the paper cited above, Lambek quotes Otto Jespersen:
In the core sciences such as physics and chemistry, practitioners do not worry about such issues.
However, the disciplines on the margins of science (such as psychology, sociology and linguistics) have spent the century in a state of anxiety over whether their core concepts and theories might turn out to be "nothing but sophistry and illusion."
This anxiety led Zellig Harris (a key figure in American structuralist linguistics and the founder of the linguistics department at Penn) to undertake a project to provide operational definitions of core linguistic concepts such as "phoneme," "morpheme," "noun," "verb" and so forth. He took the basic data to be observations of utterances, and used concepts from the then-new discipline of information theory to suggest procedures that could be used to define a hierarchy of segmentation and classification inductively. His procedures first segmented phonetic features and classifying them as phonemes, then segmented phonemes and classifying them as morphemes, and so forth.
In those days before adequate computers were accessible
(the late 1940's and early 1950's), Harris' techniques were conceptual
ones. Since then, people have tried implementing his ideas, and have found
that they work to a degree, though not entirely.
The task of providing operational definitions for the concepts of syntax -- noun, verb, sentence and the like -- was taken up by one of Harris' students, Noam Chomsky. He found the problem to be very difficult. As he worked on it, two things happened.
First, he realized that he was working on the problem of language learning. A procedure for inducing grammatical concepts from a set of utterances can be seen as a way to make linguistics respectable, by positivist standards -- but it can also be seen as an idealized or abstracted version of what a child accomplishes in learning his or her native language.
A typical child also completes this task more rapidly than Chomsky, as an adult, completed his investigation -- and Chomsky didn't actually provide a working solution. This led Chomsky to conclude that the child has an unfair advantage, that of being born with key aspects of the answer "pre-wired" by genetic endowment. But this is another topic.
Second, he explored the basic mathematics of syntax. His approach was to treat a "language" as a (typically infinite) set of strings of symbols. For instance, a "language" in this sense might be defined as the set of all strings that start with the symbol 'a', continue with zero or more copies of the symbol 'b', and then end with another 'a'. This "language" contains the strings 'aa', 'aba', 'abba', 'abbba', etc., while it excludes strings such as 'a', 'ab', 'baa', 'abc' and so on. We can summarize this language using the regular expression ab*a, where the asterisk means zero or more copies of the preceding symbol.
This is a long way from what the word language means in everyday life, just as the mathematical concept of line is quite far away from an actual line drawn in the sand or on a chalkboard. In the discussion below, we'll put the word "language" in scare quotes when we mean it in this abstract mathematical sense.
Contrary to the practice of the logical grammarians, this perspective ignores the question of meaning, and focuses exclusively on form. A "language," in this mathematical sense, has no meaning at all -- unless we provide one by some additional means.
Chomsky investigated the properties of formal systems for defining or "generating" such sets, and of abstract automata capable of determining whether a given string is a member of a particular set or not. Chomsky's generating procedures were defined in terms of rules for rewriting strings, which he called "generative grammars."
For instance, our example ab*a could be defined by a "grammar" consisting of the three rewriting rules
S -> aE
E -> bE
E -> a
Each rewriting rule says "replace the symbol(s) on the left-hand side by the symbol(s) on the right-hand side." We start by convention with a string consisting only of the symbol 'S' (for start or for sentence), and we continue applying rules until there are no more rules that apply.
There is only one rule for rewriting 'S', so we apply it to get the string 'aE'.
There is no rule for rewriting 'a' -- 'a' is a terminal symbol -- but there are two rules for rewriting 'E'. If we pick the second one, which says to rewrite 'E' as 'a', then 'aE' will become 'aa'. At this point we are done, because there are no rules for rewriting any of the symbols in the string. All of the symbols in the string are terminal symbols, and so there is nothing more that we can do.
If we go back to the string 'aE', and pick the other rewrite
rule for 'E' instead, which says to rewrite 'E' as 'bE', then our string
'aE' will become 'abE'. There are still no rules for rewriting 'a', and
'b' is also a terminal symbol, but we can continue expanding 'E'
to 'bE' if we want, giving us 'abbE', 'abbbE', 'abbbbE' and so on. At any
point along the way, we can pick the 'E -> a' rule, which will
closed off the string with a final 'a', and we will again have a string
of all terminal symbols, and be done.
1a. S -> N
1b. S -> (SIS)
2a. I -> +
2b. I -> -
2c. I -> x
2d. I -> /
3a. N -> D
3b. N -> DN
4x. D -> 0 or
1 or 2 or 3 or 4 or 5 or 6 or
7 or 8 or 9
To save space, we've used the rewrite rule labeled 4x to abbreviate the ten rules D -> 0, D-> 2, D-> 3, etc.
In this "grammar", the terminal symbols are '(', ')', '+', '-', 'x', '/', '0', '1', '2', '3', '4', '5', '6', '7', '8', '9'.
Here is a sample derivation,
based on this "grammar", that is, a sequence of string-rewriting steps
leading from the start symbol 'S' to a string containing only terminal
symbols. Each derivational step is annotated with the rule used.
At the end, we collapse six steps
to produce all the remaining digits at once, to save space in listing the
derivation.
S
(SIS)
1b
(NIS)
1a
(NI(SIS))
1b
(NI((SIS)IS))
1b
(NI((NIS)IS))
1a
(NI((NIN)IS))
1a
(NI((NIN)IN))
1a
(N-((NIN)IN))
2b
(N-((N+N)IN))
2a
(N-((N+N)xN))
2c
(D-((N+N)xN))
3a
(D-((DN+N)xN))
3b
(D-((DDN+N)xN))
3b
(D-((DDD+N)xN))
3a
(D-((DDD+D)xN))
3a
(D-((DDD+D)xDN))
3b
(D-((DDD+D)xDD))
3a
(3-((DDD+D)xDD))
4x
(3-((207+9)x14))
4x applied six times
As an exercise, play with this simple grammar long enough to see what it does and does not produce. For instance, you can see that it produces numbers like 003, starting with strings of leading zeros. Usually we don't write leading zeros in our numbers, though they do no real harm -- how might you revise the "grammar" given above so that leading zeros are not produced?
As another exercise, you might think about writing a grammar in this style for a fragment of a natural language such as English.
Chomsky's investigation brought together, in an enormously fruitful way, several strands of earlier work by logicians and mathematicians such as Turing, Church, Post, Schutzenberger (with whom Chomsky collaborated) and others. During its flowering, roughly the decade of the 1950's, it led to a set of elegant and powerful results of enormous practical importance.
Perhaps the most important result has become known as the "Chomsky hierarchy." Chomsky showed that "languages" (in the sense of sets of strings of symbols), along with their associated generative grammars and abstract automata, fall into a hierarchy of natural classes. These classes can be graded in terms of the type of rewriting rules involved in the grammar, the type of abstract automaton that is capable of determining whether a given string is "in" a given language or not, and the inherent complexity of this calculation.
Today, if you search on the web for "formal language theory"
or "Chomsky hierarchy", you will turn up thousands of pages, mostly associated
with computer science courses. These courses will
usually present the "Chomsky hierarchy" in a tabular form, something like
this:
| Language | Grammar | Machine | Example |
|---|---|---|---|
| Regular language | Regular grammar | finite-state automaton | a* |
| Context-free language | Context-free grammar | Nondeterministic pushdown automaton | a b b |
| Context-sensitive language | Context-sensitive grammar | Linear-bounded automaton | a b b c c |
| Recursively enumerable language | Unrestricted grammar | Turing machine | Any computable function |
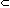 context-free languages
context-free languages 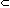 context-sensitive languages
context-sensitive languages 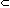 recursively enumerable languages -- where the symbol "
recursively enumerable languages -- where the symbol "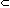 "
means "is a proper subset of".
"
means "is a proper subset of".
We are not going to try to explain the details of this
hierarchy to you. You can learn about it in several other courses at Penn,
including Ling105 and Ling106. What matters here is that there was an elaborate
mathematical development of the idea of "formal language", based on the
concepts of a set of strings generated by rewrite rules, and that out of
this development emerged a hierarchical taxonomy of basic types of formal
languages, generative grammars and abstract automata.
Chomsky's results had devastating consequences for the research program of linguistics at the time, which was dominated by a school known as structuralism. It became possible to prove mathematically that certain general types of "grammars" are inherently incapable of generating certain general types of "languages". Chomsky and his followers mounted exactly this sort of attack on structuralist linguistics, arguing that key structuralist ideas were an informal expression of "grammars" of the context-free type, and that natural language syntax is of the context-sensitive type.
Chomsky's results also suggested that hidden truths are to be uncovered by investigating the formal properties of human languages in a mathematically-precise way. The mathematical results added enormous prestige to the enterprise that gave rise to them.
Finally, Chomsky and his followers used his results to force a revolution in thinking about the epistemology of language, that is, the question of where knowledge of language comes from. It was soon shown that (under certain mathematical assumptions) the problem of learning a formal grammar from a list of examples is in principle impossible to solve. Roughly, this is because a list of possible sentences does not provide crucial "negative evidence", that is, evidence about what sentences are not possible (as opposed to just not having come up yet). This is often called the argument from poverty of the stimulus -- the input to the learning process is seen as too limited or impoverished to permit learning by a general-purpose algorithm.
Chomsky argued that this shows that children must be born with innate, genetically-programmed knowledge of what language will be like. It also follows that all languages should exhibit certain similarities, underlying their apparent vast range of differences. This gave rise to a new interest in linguistic universals.
These events produced an enormous upheaval in the intellectual landscape of several disciplines in the second half of the 20th century -- linguistics, psychology and philosophy for a start. The resulting changes are important ones, even though many of the details of the original upheaval are now a bit suspect:
As a result of the events since that time
An alphabet soup of contemporary examples:
Head-driven phrase structure grammar (HPSG)
Lexical functional grammar (LFG)
If you go on to take courses such as Ling 106 and Ling 150, you will get the background needed to understand these efforts in detail, as well as to follow the interesting twists and turns of the Chomskian linguistic enterprise over the past 40 years. For now, you may find it interesting to get a sense of what contemporary syntactic approaches are like, by browsing their web sites.