Computational Analysis and Modeling of Biological Signals and Systems
Homework 4
Due: 3/14/2022
Background for the assignment:
(See here for the actual questions, later on this page...)
The Octave or Matlab fft() function implements the Discrete Fourier Transform given by the equation
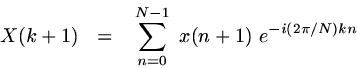
where N = length(x).
Thus for a real (or complex) input vector x of length N, fft() returns a complex vector X, also of length N.
For an explanation of why we might want to do this, see the lecture notes on "Towards the Discrete Fourier Transform". In audio applications, we usually think of the input vector x as being a sequence of sampled values in the "time domain" and the output vector X as its equivalent in the "frequency domain" -- but the idea of this transform is more abstract and general.
A simple Octave or Matlab script to implement the Discrete Fourier Transform might be
N = length(x); X = 1:N; % just to create a vector of the correct size t = 2*pi*(0:(N-1))/N; for k = 0:(N-1), X(k+1) = x*exp(-i*k*t).'; end
(assuming here that x is a row vector, i.e. a matrix of dimensions 1xN).
The Octave and Matlab implementations are a lot more efficient than this, reducing the complexity from O(N2) to O(N log N). For some details, see the Wikipedia article.
The use of X(k+1) in the script above (and in the formula it implements) reflects the fact that Octave/Matlab vectors begin with 1 rather than 0. We could equivalently have written
for k = 1:N, X(k) = x*exp(-i*(k-1)*t)'; end
This problem of whether things start from 0 or from 1 can be very confusing, and often leads to errors. In any case, for data drawn from a time function sampled at SFREQ hertz, the points of the Octave/Matlab fft(), for indices m from 1 to N/2, represent frequencies
f = (m-1)*SFREQ/N
Thus if we transform 8 samples of a signal sampled 1000 times a second, the first 4 fft points represent frequencies 0*1000/8 = 0, 1*1000/8 = 125, 2*1000/8 = 250, 3*1000/8 = 375.
The fft value at frequency 0 (Matlab or Octave index 1), being the inner product of x with exp(0*t), which is a vectors of 1's, is just the sum of the values of x. This is often referred to as "DC", for "direct current," reflecting the Electrical Engineering heritage of the terminology. If the input x is real, then this sum will obviously be real as well.
The fft value at frequency
SFREQ/2 (Matlab or Octave index (N/2)+1)
is the inner product of x with
exp(-i*(N/2)*t).
Graph the real and imaginary parts of this expression in Matlab or Octave, given
that t is as above the vector
(0:(N-1))*2*pi/N
and you will see that its real part consists of alternating 1 and -1
values, as befits a cosine wave sampled at integer multiples of pi,
and its imaginary part is always 0, as befits a sine wave sampled in
the same way. Thus this component (like the one at 0 frequency) will
always be a real number (for a real-valued input vector). Another way
to think about this case is that for a sampled sinusoid with only two
samples per period, we cannot distinguish between amplitude and phase,
as a little thought will convince you.
What about the rest of the Octave/Matlab fft() components, from N/2+2 to N? The equation given above determines their values, but we
may observe that (for real input x) they are symmetrical, in the sense
that for m from 0 to N/2-1,
X(N-m) = conj(X(m+2))
Thus for a length-8 fft,
X(8) = conj(X(2)) ,
X(7) = conj(X(3))
and
X(6) = conj(X(4)).
The values from N/2+1 to N can be treated as
negative frequencies, and a simple way to do this, putting frequency 0
in the center of the array, is the Octave/Matlab function fftshift(),
which simply swaps the left and right halves of an even-length vector.
Treating the component at N/2+1 as a negative frequency is
fine, since only the real part is non-zero, and cosine is an even
function, that is, one such that f(-t) = f(t).
The MATLAB inverse fft function, ifft(), implements the transform given by the equation
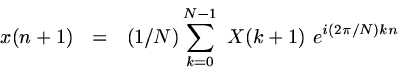
where N = length(x).
Note the two differences (other than the change of direction): the scaling factor of 1/N, and the sign change in the exponent.
QUESTIONS:
- Sine and cosine version of the DFT.
- Create a set of orthogonal basis vectors for a 16-dimensional space, using sampled sine and cosine waves of 16 frequencies. Explain each step.
- Pick three integer frequencies between 1 and 7 inclusive; pick three amplitudes and phases as you please; then create a 16-element vector f by adding up three unit-amplitude sinusoids with the chosen amplitudes and phases. (Note that this is a "time domain" vector, in the role of the input x> in the background explanation.)
- Transform f into a new 16-element vector F whose elements are the inner products of f with the 16 (sinusoidal) orthogonal basis vectors from (a) above. Do this by setting up an appropriate 16x16 transform matrix.
- From the transformed vector F, create an amplitude spectrum (that is, a vector showing the amplitude at each of the available frequencies), and a phase spectrum (that is, a vector showing the phase at each of the available frequencies). (Hint: given sine weight sw and cosine weight cw -- and assuming our sinusoids are cosines expressed as amplitude*cos(t-phase) -- the amplitude is sw*sqrt(1+((cw/sw)^2)) and the phase is atan2(cw,sw) ). What is the relationship of these spectra to the recipe that you used to create f in the first place?
- How would you translate back from F to a new version of f, fnew? Do it. Did it work?
- Use Matlab's functions fft(), abs(), and angle() to create the amplitude and phase spectrum for f ( amplitude = fftshift(abs(fft(f))), phase = fftshift(angle(fft(f))) ). How does this compare with your version? If there are differences, where do they come from?
- Implementations of sft(): the Slow Fourier Transform.
In each case below, verify that your function works correctly by comparing the transform of a random length-8 input vector (from rand(1,8)) with the results obtained from the built-in MATLAB fft().
- Write a MATLAB function sft() that directly implements the definition of the discrete Fourier transform, as in the script from the Background section above.
- Write a second version that first sets up a transform matrix
(with rows corresponding to the various values of k) and then
multiplies this matrix by the input to perform the transform.
Then either:
- Calculate the determinant of the transform matrix (using Octave or Matlab det()). What does the result mean? How would you have to change the transform definition to make the result equal to 1? OR
- Determine the effect that the matrix has on the (geometric) length of input vectors (hint: try some random inputs and compare the length of the corresponding outputs). Why do the lengths change? How could you change the matrix so that they don't? (Hint: the basis vectors in the standard dft() definition are "orthogonal" but not "orthonormal", hence the 1/N in the ifft()...)
- Write a MATLAB function isft() that directly implements an inverse discrete Fourier transform. Verify that for a random vector x, isft(sft(x)) == x.
- Magnitude and phase.
- Write a MATLAB function to convert fft output to a magnitude
and phase form. Do not use abs() and angle(),
but write the relationships out in full, to be sure that you
understand them; then you can use abs() and angle()
to check your result. Test your function by analyzing a signal
that is a length-16 vector created by summing three sinusoids
with frequencies 1, 3 and 5 (assuming a sampling frequency of
16), with random amplitudes and phases. In MATLAB, this will be
something like:
T = 2*pi*(0:15)/16; a = rand(1,3); p = 2*pi*rand(1,3) - pi; x = a(1)*cos(T+p(1)) + a(2)*cos(3*T+p(2)) + a(3)*cos(5*T+p(3));
Now verify that you can recover the frequencies, amplitudes and phases correctly from fft(x). Be aware that fft components with magnitudes that are effectively zero, but not precisely zero due to round-off error in the calculation, will have some phase or another with a value that is not very interesting. - Write a MATLAB function to display the magnitude and phase spectrum of a real signal, showing only the non-redundant values. Make sampling frequency a parameter, and number the frequency axis correctly.
- Write a MATLAB function to convert fft output to a magnitude
and phase form. Do not use abs() and angle(),
but write the relationships out in full, to be sure that you
understand them; then you can use abs() and angle()
to check your result. Test your function by analyzing a signal
that is a length-16 vector created by summing three sinusoids
with frequencies 1, 3 and 5 (assuming a sampling frequency of
16), with random amplitudes and phases. In MATLAB, this will be
something like:
- Symmetry properties:
- Construct a real, random, symmetric signal (vector x) of length 64. In MATLAB terms, ``symmetric'' here means that in the vector xx, xx[33+n] = xx[33-n] for n from 1 to 31. The point of this construction is related to the concept that we are looking at one period of a periodic signal, where we think of the first sample as being at time 0; we then ask whether the resulting (infinite-time) signal is even (symmetric, x(t) = x(-t)) or odd (antisymmetric, x(t) = -x(-t)). Look at your signal's DFT (using Matlab's FFT function). Describe what you see.
- Now do the same for a random antisymmetric real signal, and also for a random real signal that is neither symmetric nor antisymmetric.
What do you think would happen if you did these three experiments on an imaginary signal? Try it.
- Shift properties:
- Construct a real 16-element vector f with Fourier magnitude
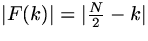 , and random phase. Do this by first
building the magnitude and phase vectors in the frequency domain
(set the 16 magnitudes according to the equation above; set the
phases by a call to rand(), except obeying the symmetry required
for a real time-domain vector, then convert to a vector of
complex coefficients), and then inverse-fourier transform (using
matlab's ifft function: f = ifft(F) ).
, and random phase. Do this by first
building the magnitude and phase vectors in the frequency domain
(set the 16 magnitudes according to the equation above; set the
phases by a call to rand(), except obeying the symmetry required
for a real time-domain vector, then convert to a vector of
complex coefficients), and then inverse-fourier transform (using
matlab's ifft function: f = ifft(F) ). - Check that the whole construction worked by Fourier transforming the resulting function and viewing the Fourier magnitude (by applying Matlab's abs function to the fft of f ).
- Now, circular-shift the signal f by N/2 samples, and again compute the Fourier magnitude and phase (in Octave or Matlab, you could implement a circular shift of N/2 samples as f1 = [f(9:16); f(1:8)], assuming that f is a column vector). How do they compare to the original? In particular, carefully compare the phase to that of the original (using Matlab's angle() function).
- What happens to the Fourier magnitude with circular shifts of other sizes?
- What happens to the Fourier magnitude and phase if you reverse f? (in Matlab, frev = f(16:-1:1) )
- (Optional) Create a new signal g[n] = f[n]
* (-1)n. That is, multiply every other sample
of f by -1. Again, compute the Fourier magnitude and
phase. How do these compare to those of the original?
Why?
Hint: you could try this with any input signal, and the result is to invert the spectrum. Just for fun, you could try it with an audio file... -- e.g. this one -- and a demo script like this:
pkg load signal [X,FS] = audioread("SA2.wav"); figure(1) specgram(X); NN=length(X); M=ones(NN,1); M(1:2:NN)= -1; IX = X.*M; figure(2) specgram(IX);
- Construct a real 16-element vector f with Fourier magnitude