Notes on Acoustics for Linguistics 520

Mark Liberman

September 10, 1990

Why Acoustics?

Acoustics is a branch of physics, and can be given only a quick overview in this course. Anyone serious about a career in phonetics should study acoustics in a more rigorous way than we can manage here. Our treatment of the subject will be spread out in time - we'll return to it throughout the course - but the course will begin with a lecture and a lab session devoted to acoustics.

This course is intended to serve the needs of someone who wants to use phonetic evidence in research on language and its use. As such a person, you need to learn enough acoustics for three purposes.

First, you should be able to engage in plausible, intuitive, semi-quantitative reasoning about the acoustic consequences of speech articulations, room acoustics, recording and transmission characteristics, etc.. Likewise, you will need to speculate intelligently about the physical cause of an observed acoustic effect. For instance, what effect is smiling likely to have on vowel formant frequencies? What are the likely acoustic correlates of pharyngeal constriction? What causes the lowered first formant in the vowels that follow Javanese ``heavy'' consonants? It is possible to discuss these questions in an informed way without being able to manipulate the equations for even a simple model of the human vocal tract.

Second, you need to be able to make an intelligent choice of options for acoustic analysis and display, and you need to be able to make a sensible interpretation of the results of such an analysis. For instance, how should you look for voice pitch in a time waveform? How should you make a spectrogram in order to see pitch-related phenomena for a very low-pitched voice? What does it mean if the vertical pitch striations in the wide-band spectrogram of a high-pitched voice seem to blur together, and simultaneously some regular horizontal bands appear? Could a certain white patch on the spectrogram be due to room acoustics? These questions also require at least a ``cookbook'' level of understanding of acoustic signal processing, which in turn cannot be understood without some elementary understanding of the acoustic physics that lies behind the signals being processed.

Third, you need to understand how acoustic signals are processed in the peripheral auditory system, in order to have an informed opinion about the likely perceptual significance of articulatory and acoustic variation.

Use of Mathematics

Our treatment of acoustics will use simple mathematical formulae where they are the best way to express the ideas in question. Certain other parts of the course, especially the discussions of signal processing and of statistical analysis, will similarly involve some mathematical formalism. If you have any trouble with the mathematics used in these lecture notes, tutoring help is available on request.

Sound and other waves

Most of this should be simple review for those who have had at least a high school physics course, and can remember its contents. For others, I would suggest some supplementary reading in a physics textbook.

Sound in air consists of longitudinal (or compressional) waves.

A wave is an influence or disturbance that starts at some point and travels to another point in a way that depends on the physical properties of the medium through which it is transmitted, leaving the medium essentially unchanged. Thus ocean waves do not transport water onto the shore, and sound waves do not build up air in your ear.

In a longitudinal wave, the particles of the transmitting medium move in the direction of the wave motion. Note that since the medium itself remains in place, the particles must move back and forth.

There are many other kinds of waves. Solids carry not only longitudinal waves, but also several kinds of transverse waves, in which particles move at right angles to the direction of wave motion; these different kinds of waves typically travel independently at different speeds. Shaking a stretched rope produces a flexural transverse wave; torsional transverse waves, in which a twisting distubance propagates through a solid body, also exist. Electromagnetic waves act like transverse waves propagating in a non-existent ether. Surface waves in deep water have both longitudinal and transverse components, so that each particle follows a circular path; breaking waves in shallow water are considerably more complex.

Air is made up of molecules and atoms of various gases constantly flying around in all directions, and a sound wave in air is a disturbance propagated by these particles bumping into one another. Since very large numbers of particles are involved (a cubic millimeter of air contains a million times more molecules than there are people on earth), it's reasonable to treat air for acoustical purposes as homogeneous, ignoring the details of the actual particles involved. The same is true for other materials - when an acoustical explanation refers to a particle, what is meant is just a small piece of such a homogeneous medium.

In fact, for sound as we know it to exist in a gas, we must be dealing with a spatial scale that is large compared to the distance that individual molecules typically travel before bumping into each other (the mean free path). This is because to have the propagation of a disturbance in pressure that we know as sound, we want an object to move against the air rapidly enough to compress it, and we want this pressurized air to push on the air next to it, which is in turn compressed, and so on. But if we have an area with a higher density of molecules next to an area with a lower density of molecules, the molecules will move out of the region of higher density so as to equalize the difference. If this is able to happen, the densities and pressures will equalize, and there will be no pattern left to propagate. In order to get sound, the molecules rushing out of the area of higher density must bump into the molecules in the area of lower density and transfer momentum to them.

Units of Pressure

There are two different sets of units in use in scientific measurement: the SI system and the CGS system. Since you may encounter both in your reading, you have to learn both. The most important thing, though, is to learn the basic definitional nature of the quantities involved, which is to say, the way that they are defined in terms of other quantities. Thus pressure is a measure of force per unit area.

Since (in the SI system) force is measured in newtons, and area in square meters, pressure is measured in newtons per square meter, N/m². A newton is one $kg\;m/{s^2}$ (remember, by Newton's Second Law, force equals mass times acceleration. Since the acceleration of the earth's gravity at its surface is about 9.81 m/s², a one kilogram mass sitting on a table presses down with a force of about 9.81 newtons (confusingly enough).

The unit of force in the CGS system, the dyne, is 10^-5 newtons.

One pascal (abbreviated Pa) is one N/m². One bar (or 1000 millibars) is $10^{5} \; N/m^2$.

Normal atmospheric pressure (``one atmosphere'') is almost the same: 1 atm is 1.0133 bars. This is a static pressure -- at time scales involved in analyzing sound, it doesn't change.

The pressure variations in air caused by sound wave at comfortable listening levels range from about .01 to 1 N/m², or 10^-7 to 10^-5 atmospheres (atm.). The instantaneous sound pressure is the total instantaneous pressure minus the static pressure. The effective sound pressure is the root mean square of the instantaneous pressure over an appropriate time.

The Speed of Sound

Sound propagates at a speed that depends on an inertial property of its medium (how hard you have to push to get a bit of the medium to move) and also on an elastic property of its medium (to what extent a bit of the medium passes a push onto the next bit, instead of compressing in on itself). The inertial property is just the volume density $\rho$, that is, the mass per unit volume. The elastic property is known as the bulk modulus B, defined as the ratio of a change in pressure $\Delta p$ to the corresponding fractional change in volume $\Delta V / V$, with a minus sign to make B a positive quantity:

$$B = -{\frac{\Delta p}{\frac{\Delta V}{V}}}$$

For conditions in which the disturbance passes rapidly enough that no heat transfer takes place from one part of the medium to another (adiabatic conditions), the speed of sound v is then given by the equation

$$v = \sqrt{\frac B \rho}$$

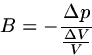
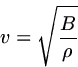
The speed of sound in a number of media is given in the following table:

1|c|Material 1c|Temperature (C) 1c|Speed (m/s)

Air 331

Air 20 343

Helium 965

Hydrogen 1284

Carbon Dioxide 258

Water 1402

Water 20 1482

Seawater (3.5% salinity) 20 1522

Methyl Alcohol 1130

Aluminum -- 6420

Steel -- 5941

Granite -- 6000

Brass -- 3480

Lead -- 1210

Glass -- 1c|3700-5000

The speed of sound in a gas is unchanged by a change in pressure, since B and $\rho$ are increased in the same proportion by an increase in pressure.

However, an increase in temperature causes an increase in the speed of sound in a gas, since the gas expands and its density is decreased; over the range of temperatures humans live in, the speed of sound in air increases by about .6 m/s for each degree centigrade, so that if t is the temperature in degrees centigrade, the speed of sound in dry air is approximately given by the equation

$$v = 331 + .6 t \; m/s$$

Derivation of the speed of sound from Newton's second law

In 1687, Newton tried to derive the speed of sound in air from three sets of elementary philosophical principles, namely the principle of the conservation of mass, the law that force equals mass times acceleration, and the law relating pressure, temperature and volume for an ideal gas. Even today, we should be able to sense the breathtaking audacity of this effort, and our admiration is, in a sense, only increased by the fact that Newton got it wrong.

Consider the assumptions that he started with: matter is neither created nor destroyed; force is the product of mass and acceleration; the volume of a gas is inversely related to its pressure, if temperature is held constant. From only these assumptions and no others, he derived the equations governing the propagation of sound, and predicted the speed of sound.

The form of his argument was essentially valid, but he assumed that the propagation of sound was isothermal, i.e. that the temperature of the conducting medium remained constant. In the large, this is true; if we ignore the dissipation of energy through frictional losses, as Newton did, the passage of an idealized sound wave through an idealized compressible medium leaves the same temperature behind that prevailed before. However, the compressions and rarefactions that represent (even lossless) passage of sound through air occur too rapidly for any significant amount of equalization of temperature to take place between the regions of temporarily higher pressure and the regions of temporarily lower pressure. This state of affairs, which is called adiabatic, was not recognized until 1807, when Laplace figured it out.

With Newton's (incorrect) assumption of isothermal conduction, the speed of sound in a compressible medium turns out to be simply (if incorrectly)

$$v = \sqrt{\frac P \rho}$$

where P is the static pressure of the medium and $\rho$ is its static density. For air at standard temperature and pressure, P is $1.0135 \times 1-^5 N/m^2$, and $\rho$is 1.2933 kg/m³, so this gives a value of 279.95 m/sec for the speed of sound. This is about 16% less than the true value of 331 m/sec.

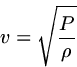
Can you think of an experiment that Newton might have conducted, in 1687, that would have determined the speed of sound in air with greater accuracy than this?

The extraordinary thing is that Laplace's correction of Newton's argument--which remains a breathtakingly simple argument from the most fundamental principles, applied to a ruthlessly simple model of what sound is and how it propagates--does produce values quite close to experimental observation.

Linearity I

Sound waves in air have the property that they travel at the same speed regardless of the shape or time course of the disturbance involved; especially, sounds of different pitches travel at the same speed. Another way of saying this is that air is a nondispersive medium.

As a result, the propagation of sound waves in air is quite simple. In the simplest case, that of a plane wave, if we consider the pattern of pressure in time along a single dimension x, then if some feature of the pattern is at point x₁ at time t₁, at a later time $t_2 = t_1 + {\Delta t}$ the same feature will be at the point $x_2 = x_1 + v\,({\Delta t})$, and the pattern of pressure around the point x₂ at t₂ will be identical to the pattern around x₁ at t₁. In such a case, the wave equation is linear, which means that the principle of superposition holds, with various nice results. Linearly-propagating sound waves from multiple sources simply add, so that if one sound can be described as p = f(x,t) and a second sound can be described as p = g(x,t), then the two sounds together make the pattern p = f(x,t) + g(x,t). By the same token, sounds traveling in different directions pass through one another without being changed; and more. Actual sound waves are generally spherical waves, which decay in amplitude according to an inverse square law as they radiate out from their source; but their propagation remains linear. If we consider a small piece of a spherical sound wave some distance from its source, we can approximate it pretty well over a short distance as a plane wave. In a tube-like structure such as the human vocal tract, for sound patterns whose spatial extent is large compared to the diameter of the tube, a model based on plane waves also gives a pretty good approximation.

Periodic waves: frequency, period and wavelength

Some sound waves are (at least approximately) periodic - that is, their time-varying pattern of variation in pressure repeats itself after a certain time, over and over again. The repetition time of a periodic sound wave is called its period. A one-dimensional periodic wave p = f(x,t) with a period $\tau$,examined over the spatial dimension x at times t₁, $t_1+ \tau$, $t_1+2 \tau$, $t_1+3 \tau$ etc. will thus show exactly the same spatial pattern. In fact, for any integer n, the pattern $f(x,t_1+n \tau)$ will always be the same. Another way to say the same thing is that a certain point in the spatial pattern of the wave (say a pressure maximum) will pass a given point in space every $\tau$ seconds.

Instead of the period $\tau$, which is the time between repetitions, we can equivalently talk about the frequency f, which is the number of repetitions per second. Obviously

$$f = \frac{1}{\tau}$$

by definition.

Due to the previously-mentioned linearity of propagation, the pattern of a periodic wave p = f(x,t) also repeats itself exactly in space. At a fixed time, if we start at point x₁ and look along the x dimension a distance $v \tau$, where v is the speed of sound and $\tau$ is the period of the wave, we will find the point that used to be at x₁ at a time $\tau$ seconds earlier, which by definition has an identical value. Thus for any integer n, the time-varying pattern $f(x_1+nv \tau,t)$ will always be the same. The wave's interval of repetition in the spatial dimension, $v \tau$, is called its wavelength, and is usually represented as $\lambda$. Thus definitionally

$$\lambda = v \tau$$

and

$$\lambda = \frac{v}{f}$$

for wavelength $\lambda$, speed of sound v, period $\tau$, and frequency f.

Pressure and particle velocity

Sound intensity and power

If p is sound pressure, $\rho$ is air density, particle velocity is u, particle displacement is d, and c is the speed of sound, then

$$p = \rho c u$$

and (incidentally)

$$d = \frac{u}{2 \pi f}.$$

For a plane wave, the intensity or sound power I is

$$I = p u = \frac{p^2}{\rho c} = \rho c u^2.$$

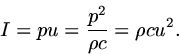
As a measure of power per unit area, sound intensity can be denominated in watts per square meter. This brings up the fact that to create and propagate sound, a disturbance in a physical medium, involves the expenditure and transmission of energy. The process by which energy is carried away from a sound source through a medium is called radiation. A large orchestra playing at maximum volume radiates about 60 or 70 watts of sound power; a piano can produce about half a watt.

Under conditions in which sound waves radiate from their source in an expanding spherical shell, the power per unit area at a distance R of a source radiating P watts of acoustic power is

$$I = \frac{P}{4 \pi R^2}.$$

Therefore the sound intensity measured at a distance of 5 meters from a source radiating one acoustic watt of power is

$$I = \frac{1}{4 \pi 5^2}$$

or about .003 watts per square meter. Note however that inverse-square-law conditions are rarely found, due to directional radiation, reflections from obstacles, etc.

Because sound intensities (as well as sound pressures and other such measures) vary so widely, it is normally more useful to treat them on a logarithmic scale as intensity levels. Thus we measure sound intensity level (SL) in decibels or dB, defined as $10 \log _ {10}$ of the ratio of the sound intensity to some reference level. Note that a bel is a dimensionless unit that is simply the log to the base 10 of an arbitrary intensity ratio, with the factor of 10 coming along with the metric prefix deci-. Thus we can use dB to measure levels of voltage or luminance or pressure or any other quantity, as long as we define a suitable reference level, and modify the equation as needed to be sure that we dealing with a ratio of intensities (where intensity is power per unit area).

The usual reference level for sound intensity is 10 -12 watts per meter squared. Thus .003 watts per meter squared would be a sound intensity level IL of

$$IL = 10 \log _ {10} (\frac{.003}{10^{-10}}) = 94.77 \;dB$$

If we are dealing with ratios of currents, voltages, pressures, volume currents, forces, particle velocities etc., which are square roots of power, then intensity level in dB becomes $20 \log _{10}$of the ratio of these quantities, the additional factor of 2 outside the log serving to square the quantity whose log is being taken.

The reference level for sound pressure is $2 (10)^{-5} \; N/m^2$.

Recall that the effective sound pressure is the RMS of the instantaneous sound pressure over an appropriate time.

Mathematical description of a plane wave

We consider a plane sound wave, for instance a wave traveling through a long tube filled with air. The variable x will represent position along the length of this tube, and the variable t will represent time. Because it is a plane wave, we are assuming that the state of compression or rarefaction of the air in the tube at a given value of x is the same regardless of whether it is measured in the middle of the tube or close to the walls; in other words, the wave is one dimensional, in the sense that the pressure varies only as a function of the single spatial variable x, with no variation occuring in the other two dimensions of space. In fact, we call it a plane wave because the wavefront -- the traveling region of air compressed to an equal degree - is modeled as a plane moving down the tube. (A geometric flat surface, not an aircraft!) This idealization is not in fact likely to be true in the real world, but it simplifies the mathematics considerably; in addition, as long as we are dealing with wavelengths that are large compared with the width of the tube, a one-dimensional model will match experimental observation quite well.

As another simplifying idealization, we imagine that the wave propagates to infinity without any change -- needless to say, real waves die out gradually due to losses of various sorts, even if they are not changed more abruptly by running into something (like the end of the tube!).

Let a ``particle'' of air at position x have a time-varying longitudinal displacement  

$$d = d_{\max}\cos(kx - \omega t)$$ (1)

Since the cosine function varies between 1 and -1, the maximum displacement value $d_{\max}$ will scale the displacement to the specified value. The variable k is a way of defining the scale of the x dimension. We can see its effect clearly by setting t=0, in which case equation 1 becomes $d = d_{\max}\cos(kx)$,and k specifies how many complete periods of the wave will occur in each $2\pi$ of distance along the dimension x. Thus k times the wavelength $\lambda$ equals $2\pi$, and

$$\lambda = \frac{2\pi}{k}$$

The constant k is known as the angular wave number, and its units are radians per meter. It is sometimes convenient to refer to the wave number of a wave, symbolized $\kappa$, and giving the number of wave periods per unit length:

$$\kappa = \frac{1}{\lambda} = \frac{k}{2\pi}$$

In order to understand the meaning of the constant $\omega$in equation 1, set the spatial variable x to 0, which turns the equation into $d=d_{\max}\cos(- \omega t)$. Since the cosine function is symmetrical around zero, we can eliminate the minus sign, giving us $d=d_{\max}\cos(\omega t)$.This equation shows us the variation of displacement over time of the ``particle'' of air at position x=0. We can see that $\omega$ is scaling the wave pattern in time just as k scaled it in space -- $\omega$ specifies how many complete periods of the wave will occur per $2\pi$ seconds of time, and is therefore known as angular frequency, denominated in units of radians per second. Again, $\omega$ multiplied by the period $\tau$equals $2\pi$, and so

$$\tau = \frac{2\pi}{\omega}$$

and the frequency f is given by

$$f = \frac{\omega}{2\pi}$$

Note that the information provided by k and omega about the wave's scale in space and time is equivalent to (in the sense of being interdefinable with) the information provided by knowledge of frequency and wavelength, or frequency and the speed of wave propagation, or whatever. Thus the speed of wave propagation can be expressed as

$$c = \frac{\omega}{k} = \frac{\lambda}{\tau} = \lambda f$$

We can derive this from simple consideration of the definitions of the quantities involved; but there is another important way to look at the derivation of a velocity from equation 1. The value defined by equation 1 is determined by the value inside the cosine function, so that we can define the values of x and t for which the wave displacement has a particular characteristic, say a maximum or a minimum, in terms of some constant value of the expression $kx-\omega t$. To look at how the wave evolves in time, we can track the motion of our chosen feature as we change t by a small amount, just by adjusting x so as to keep $kx-\omega t$ constant. The amount of change in x per unit change in t that we have to make in order to maintain $kx-\omega t$ at some constant value (call it M) is clearly just a definition of the velocity at which the wave moves in the x dimension. The limit of ${\Delta x}/{\Delta t}$for $kx-\omega t = M$, as $\Delta t$ gets smaller and smaller, is just the derivative of $kx-\omega t = M$, which is

$$k\frac{dx}{dt} - \omega = 0,$$

so that

$$\frac{dx}{dt} = \frac{\omega}{k}$$

Even without this simple application of calculus, we can see that if we increase t (thus increasing time) in the expression $kx-\omega t$, we will have to also increase x in order to keep the expression constant, so that the wave is seen to be moving in the direction of increasing x.

What should we do to equation 1 to get the wave to move in the other direction, so that if we follow a certain feature of the wave shape through time, the value of spatial variable x will be decreasing? Simple: we just replace $kx-\omega t$ with $kx+\omega t$ -- all the discussion of the meaning of k and $\omega$ remains basically unchanged, but now if we increase t by a little bit, we will need to decrease x in order to keep $kx+\omega t$ at a constant value. The time derivative now becomes

$$\frac{dx}{dt} = -\frac{\omega}{k},$$

with the negative velocity representing motion at the same speed as before, but in the direction of decreasing x.

Sound pressure and displacement

All of the previous discussion of the equation for a one-dimensional sound wave was expressed in terms of the displacement of a ``particle'' or small packet of air. The expression for the corresponding sound pressure, that is the change in pressure above and below the pressure prevailing in the absence of sound, is  

$$\Delta p = {\Delta p}_{\max}\sin(kx - \omega t)$$ (2)

Here $\Delta p$ is the sound pressure, ${\Delta p}_{\max}$ scales the maximum sound pressure, and the meaning of k and $\omega$ is the essentially same as before. Likewise, the discussion of velocity and direction of propagation is essentially the same.

Note that displacement and pressure variation are $\frac{\pi}{2}$ out of phase; that is, the pressure variation is 1/4 wavelength ahead of the displacement variation, so that sound pressure is zero when the displacement is at a maximum or minimum, and vice versa. Intuitively, you can think of an air particle in a maximum compression as standing still in the middle of its neighbors rushing in on it from the two sides, and an air particle in a maximum rarefaction as standing still while its neighbors rush away from it.

Standing waves

We have been discussing ``traveling waves,'' the normal kind of sound waves that propagate through a medium. Another common kind of sound wave is a ``standing wave,'' a periodic disturbance of a medium that remains fixed in space even though it varies in time.

We learned that traveling sound waves arise because things--particles of the medium--bump into each other, transmitting a disturbance through space at a rate that depends on the density and elasticity of the medium. What about standing waves? In general, they arise through the interaction--or ``interference''--of two or more traveling waves.

Here is a simple algebraic demonstration that two sine waves of equal frequency and amplitude traveling in opposite directions produce a standing wave, that is, a pattern which repeats periodically over time but does not propagate in space.

From the previous discussion, we know that a sine wave moving in the positive direction has an equation of the form

$$y_{pos} = a\sin(kx - \omega t),$$

while a sine wave moving in a negative direction has the form

$$y_{neg} = a\sin(kx +\omega t).$$

In each case, the equation defines the value of instantaneous sound pressure as a function of position x and time t. By the principle of superposition, the two waves together simply add:  

$$y = a\sin(kx - \omega t) + a\sin(kx + \omega t)$$ (3)

Since for all $\alpha$, $\beta$

$$\sin \alpha + \sin \beta = 2\sin \frac{1}{2} (\alpha+\beta)\cos\frac{1}{2}(\alpha-\beta)$$

equation 3 can be rewritten as  

$$y = 2a\sin k x \cos \omega t$$ (4)

When x has the values 0, $\pi$, $2\pi$, and so on, equation 4 will be zero no matter what the value of t is. These x values define points in space that are the (pressure) nodes of the standing wave, the places where there is never any variation. When x has the values $\frac{\pi}{2}$, $\frac{3\pi}{2}$,and so on, equation 4 can have a value between -1 and 1, depending on the value of the cosine term, which oscillates in a way that varies with time but does not depend on spatial position. These x values define the (pressure) antinodes of the standing wave, where the sound wave's pressure varies with time between a maximum and a minimum value. Points near the antinodes vary in the same way, but between smaller maximum and minimum values, with the extremal values getting smaller and smaller as we move away from a antinode and towards an node.

Note that sound pressure and (air-particle) displacement are ``opposite'' here. Thus a node of the pressure standing wave, where there is no pressure variation at all, will be an antinode of the displacement standing wave, where the air particles are moving freely back and forth to the maxium extent. Similarly, an antinode of the pressure standing wave, where the pressure is varying to the maximum extent, will be a node of the displacement standing wave, with an air particle at that point remaining fixed in space as its neighboring particles push back and forth against it from both sides.

Physical interpretation of standing waves

How could this situation--two sine waves of equal frequency and amplitude tranveling in opposite directions--actually arise?

Well, we could try to set it up by installing two loudspeakers facing each other, etc. This would work just fine, but it is not a circumstance that often arises in nature. For a commoner cause of standing waves (in fact one that is ubiquitous), consider the reflection of a sound wave from a hard surface like a wall.

If the reflection were perfect, then an exact copy of the incident wave would be reflected back in the opposite direction, and we would have the basic standing wave situation exactly. Real reflections are not by any means perfect--some of the wave's energy is always absorbed rather than being reflected back--but actually this does not change the situation very much. Suppose that the incident wave is reflected back with half of its original amplitude. Conceptually, we can subdivide the incident wave in two equal parts, one of which will interact exactly with the reflection to produce a standing wave, while the other one is absorbed. Thus we can describe the resulting situation as a standing wave with half the amplitude of the incident wave, superimposed on a traveling wave, also with half the amplitude.

In the physical world, reflections of sounds waves in air occur everywhere, all the time. Reflections occur from ``hard'' surfaces--and human flesh is hard enough to generate pretty good relections of sound waves, a fact that is crucial to the existence of speech as we know it. In most situations that we find ourselves in, an acoustic disturbance will reflect multiple times before it dies away completely. If we have two reflective surfaces facing each other, a sound may bounce back and force between them quite a number of times.

All surfaces absorb at least a little bit of the energy of an incident sound waves, and some energy is also lost through heating the medium of transmission, so we must reject Chaucer's idea that sounds bounce around indefinitely until they find their way to a sort of acoustic valhalla. Still, appropriate configurations of reflective surfaces tend to set up standing waves that persist long enough to have a noticeable effect. This is especially true if there is a persistent source of acoustic energy to interact with the patterns of reflection that produce a standing wave.

As an aside, we should note that sound waves reflect not only in circumstances that create increased local pressure (such as collision with a hard surface) but also in circumstance that create decreased local pressure (such an opening from a smaller chamber into a larger one). You can see this most clearly if you imagine holding onto a piston that can slide in a cylinder full of air: if you push in on the piston, you create an positive pressure that will propagate through the air in the cylinder, while if you pull out on the piston, you create a negative pressure that will also propagate through the air in the cylinder in the same way.

Models of resonance

Standing waves set up by sound waves bouncing around in enclosed areas (like the mouth!) are one kind of ``resonance'' phenomenon.

As an illustration of the concept of resonance, think about pushing someone on a swing. The swing naturally wants to swing back and forth (``oscillate'' in more technical language) at a certain frequency, depending on how long the rope is. If you push the swing, it starts to oscillate at this natural frequency. If you push repeatedly and regularly, what happens depends on whether you make your pushes in synchrony with the swing or not. If you push at the right times, your pushes add energy to the swing, and it swings higher; if you push at the wrong times, the swing loses energy to you, and it swings lower.

The swing is a particularly simple example of a resonating system. All physically oscillating systems have such natural patterns of oscillation, or resonances. In most cases, a system has multiple resonances--multiple natural modes of oscillation, multiple ways that the system ``wants'' to oscillate. Usually (in fact always for spatially-localized systems) these natural modes are quantized. Just as in the case of the swing, input energy at one of the resonance frequencies will be transferred efficiently into oscillation of the system, while input energy at other frequencies will not.

In some simple systems, we may be able to figure out what the quantized resonances will be, by considering properties of the corresponding standing waves. For instance, consider the patterns of oscillation that can arise when we pluck a stretched string. A local disturbance will propagate along the string, just like a local disturbance propagates in air; that is, the string serves as the medium for a wave. If the ends of the string are fixed, then the waves will reflect back from the ends--think about wiggling a rope that is tied to the wall at one end.

The result will be a set of standing waves on the string, patterns of motion that vary in time but are fixed in space (with respect to position along the string, at least). Where are the nodes and antinodes of these standing waves? We know that the ends of the string are fixed in space, by hypothesis, and so these points must be (displacement) nodes of the standing waves. In fact, this ``boundary condition'' is all that we need to know: the possible modes of resonance of the string are all and only the standing waves whose (displacement) nodes are at the ends.

The lowest (spatial) frequency (sinusoidal) standing wave meeting these boundary conditions will be one in which the length of the string l is half of the wavelength $\lambda$, so that $\lambda~=~2l$. The next one will have l equal to one full wavelength, so that $\lambda ~=~ l$, and then l equal to one and one half wavelengths, so that $\lambda ~=~ \frac{2l}{3}$, and so on. The set of possible standing waves will thus have wavelengths $\lambda~=~\frac{2l}{N}$, for $N~=~1,2,3,4, \ldots$. The corresponding frequencies will be

$$f ~=~ \frac{Nc}{2l}, ~~~~~N~=~1,2,3,4, \ldots$$ (5)

Thus if the frequency of the standing wave with the largest wavelength (and thus the lowest frequency) is f₁, then the other standing waves will be at all integer multiples of f₁.

Note that these standing waves represent possible resonances or natural oscillation-patterns of the string--which if any of them will actually be set in motion, and to what extent, depends on how the string is plucked or otherwise excited.

Resonance in simple acoustic tubes

Consider the case of sound waves propagating inside a tube that is closed at both ends. We assume that the ends reflect sound waves, and so we know that these patterns will be able to set up a standing wave pattern inside the tube. What standing wave patterns are possible in this case?

We can make a very similar argument to the one made above for the string. The closed ends of the tube are like the fixed ends of the string: the particles of air at the ends cannot move, so these must be displacement nodes, and therefore pressure antinodes. Thus the possible standing waves will be just like those possible on the string: wavelengths $\lambda~=~\frac{2l}{N}$, for $N~=~1,2,3,4, \ldots$,or frequencies $f~ =~ \frac{Nc}{2l}, N~=~1,2,3,4, \ldots$

A tube with both ends open ends up showing just the same pattern: here we are relying on the ``negative reflection'' caused by the opening of the ends of the tube, and the ends must now be displacement antinodes. The wavelengths of the possible standing waves will be just the same as the case in which both ends are closed.

What if one end of the tube is open, and one is closed?

In this case, the boundary conditions tell us that the possible standing waves are those in which there is a displacement node at one end, and a displacement antinode at the other end. Inspection of a sinewave plot shows us that the longest-wavelength standing wave consistent with this condition will be one whose wavelength is four times the length of the tube. The next will one whose wavelength is 4/3 the length of the tube, and then 4/5. In general, the standing waves in this case will have wavelengths

$$\lambda ~=~ \frac{4l}{N},~~~N~=1,3,5,\ldots$$ (6)

and corresponding frequencies

$$f ~=~ \frac{Nc}{4l},~~~N~=~=1,3,5,\ldots$$ (7)

As we will see later on, the human vocal tract is reasonably well modeled for some purposes as an acoustic tube closed at one end and open at the other, so that this last case is of particular interest.

Other Reading

You may find it helpful to read some sections of a college physics textbook, for instance chapters 14, 17 18 of ``Fundamentals of Physics,'' Halliday and Resnick, 1988.

Footnotes

...function

Later in the course, we will see why it is a good idea to use represent waves using sine and cosine functions as primitive ``building blocks.'' Meanwhile, you need an intuitive understanding of the basic nature of these functions.